ریاضیات

الگوریتم Dijkstra-

• الگوریتم Dijkstra یک الگوریتم حریص بسیار معروف است.
• برای حل مسئله کوتاهترین مسیر تک منبع استفاده می شود.
• این کوتاهترین مسیر از یک گره منبع خاص به سایر گره های باقی مانده نمودار را محاسبه می کند.

همچنین بخوانید - کوتاهترین مسیر مسیری

شرایط-

توجه به نکات زیر در مورد الگوریتم Dijkstra مهم است -

• الگوریتم Dijkstra فقط برای نمودارهای متصل کار می کند.
• الگوریتم Dijkstra فقط برای آن نمودارهایی که حاوی هیچ لبه وزنی منفی نیستند کار می کند.
• الگوریتم واقعی Dijkstra کوتاهترین مسیرها را تولید نمی کند.
• این فقط ارزش یا هزینه کوتاهترین مسیرها را فراهم می کند.
• با ایجاد تغییرات جزئی در الگوریتم واقعی ، به راحتی می توان کوتاهترین مسیرها را بدست آورد.
• الگوریتم Dijkstra برای نمودارهای جهت دار و همچنین جهت دار کار می کند.

الگوریتم Dijkstra-

dist [ S ] ← 0 // فاصله تا راس منبع روی 0 تنظیم شده است

Π [ S ] ← NIL // سلف رأس منبع به عنوان NIL تنظیم شده است

برای همه v ∈ V - { S } // برای همه رئوس دیگر

do dist [ v ] ∞ // تمام فاصله های دیگر روی to تنظیم شده است

Π [ v ] ← NIL // سلف سایر رئوس به عنوان NIL تنظیم شده است

S ← ∅ // مجموعه رئوس بازدید شده از "S" در ابتدا خالی است

Q ← V // صف 'Q' در ابتدا شامل همه رئوس است

while Q ≠ ∅ // while حلقه اجرا می شود تا صف خالی نباشد

انجام U ← mindistance ( Q، ناحیه ) // یک راس از Q با حداقل فاصله است انتخاب <فونت> در

S ← S ∪ { u } // Vertex 'u' به لیست "S" رئوس بازدید شده اضافه می شود

برای همه همسایگان v [ u ] // برای همه رئوس همسایه راس 'u'

انجام اگر ناحیه [ V ] > ناحیه [ U ] + W ( u و v ) // اگر هر کوتاهترین مسیر جدید کشف میشود <فونت> در

سپس dist [ v ] dist [ u ] + w ( u، v ) // مقدار جدیدترین کوتاهترین مسیر انتخاب می شود

بازگشت dist

پیاده سازی-

نحوه اجرای الگوریتم Dijkstra فوق در مراحل زیر توضیح داده شده است -

مرحله 01:

در اولین قدم دو مجموعه تعریف شده است -

• یک مجموعه شامل تمام رأس هایی است که در درخت کوتاه ترین مسیر قرار گرفته اند.
• در ابتدا ، این مجموعه خالی است.
• مجموعه دیگر شامل تمام رأس هایی است که هنوز باقی مانده اند تا در درخت کوتاه ترین مسیر قرار گیرند.
• در ابتدا ، این مجموعه شامل تمام رئوس نمودار داده شده است.

مرحله 02:

برای هر راس نمودار داده شده ، دو متغیر تعریف شده است

• Π [v] که سلف راس 'v' را نشان می دهد
• d [v] که کوتاهترین مسیر تخمین راس "v" از راس منبع را نشان می دهد.

در ابتدا ، مقدار این متغیرها به صورت زیر تنظیم می شود:

• مقدار متغیر 'Π' برای هر راس روی NIL یعنی Π [v] = NIL تنظیم می شود
• مقدار متغیر 'd' برای راس منبع 0 تنظیم شده است یعنی d [S] = 0
• مقدار متغیر 'd' برای رئوس باقیمانده روی ∞ یعنی d [v] = set تنظیم شده است

مرحله 03:

روش زیر تکرار می شود تا زمانی که تمام رئوس نمودار پردازش شوند -

• از میان رئوس پردازش نشده ، یک راس با حداقل مقدار متغیر "d" انتخاب می شود.
• لبه های خروجی آن آرام است.
• پس از آرام کردن لبه های آن راس ، مجموعه های ایجاد شده در مرحله 01 به روز می شوند.

آرامش لبه چیست؟

لبه (a ، b) را در نمودار زیر در نظر بگیرید -

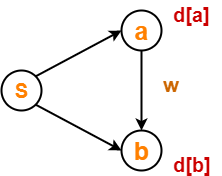
در اینجا ، d [a] و d [b] نشانگر کوتاهترین برآورد مسیر برای رئوس a و b به ترتیب از راس منبع 'S' است.

اکنون،

اگر d [a] + w

سپس d [b] = d [a] + w و Π [b] = a

این به عنوان آرامش لبه نامیده می شود.

تجزیه و تحلیل پیچیدگی زمان-

Case-01:

این مورد معتبر است وقتی-

• نمودار داده شده G به عنوان یک ماتریس مجاورت نشان داده شده است.
• صف اولویت Q به عنوان یک لیست غیر مرتب نشان داده می شود.

اینجا،

• A [i، j] اطلاعات مربوط به لبه (i، j) را ذخیره می کند.
• زمان لازم برای انتخاب i با کمترین فاصله O (V) است.
• برای هر همسایه i ، زمان لازم برای به روزرسانی dist [j] O (1) است و حداکثر همسایگان V وجود دارد.
• زمان لازم برای هر تکرار حلقه O (V) است و یک راس از Q حذف می شود.
• بنابراین ، پیچیدگی زمان کلی به O (V 2 ) تبدیل می شود .

مورد 02:

این مورد معتبر است وقتی-

• نمودار داده شده G به عنوان یک لیست مجاورت نشان داده شده است.
• صف اولویت Q به عنوان یک انبوه دودویی نشان داده می شود.

اینجا،

• با نمایش لیست همجواری ، تمام رئوس نمودار را می توان با استفاده از BFS در زمان O (V + E) پیمایش کرد.
• در min heap ، عملیاتی مانند استخراج دقیقه و مقدار کاهش کلید زمان O (logV) را می گیرند.
• بنابراین ، پیچیدگی کلی زمان O (E + V) x O (logV) می شود که O ((E + V) x logV) = O (ElogV) می شود
• این پیچیدگی زمانی را می توان با استفاده از پشته فیبوناچی به O (E + VlogV) کاهش داد.

مشکل تمرین مبتنی بر الگوریتم DIJKSTRA-

مسئله-

با استفاده از الگوریتم Dijkstra ، کمترین فاصله راس منبع "S" تا رئوس باقی مانده را در نمودار زیر پیدا کنید -

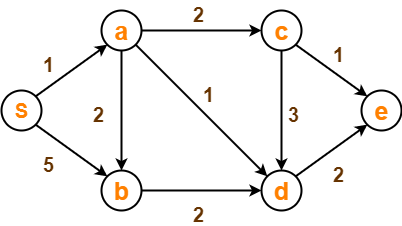
همچنین ترتیب بازدید از رئوس را بنویسید.

راه حل-

مرحله 01:

دو مجموعه زیر ایجاد شده است-

• مجموعه بازدید نشده: {S ، a ، b ، c ، d ، e}
• مجموعه بازدید شده: {}

مرحله 02:

دو متغیر Π و d برای هر راس ایجاد می شوند و به صورت اولیه تنظیم می شوند

• Π [S] = Π [a] = Π [b] = Π [c] = Π [d] = Π [e] = NIL
• d [S] = 0
• d [a] = d [b] = d [c] = d [d] = d [e] =

مرحله 03:

• Vertex 'S' انتخاب شده است.
• دلیل این امر این است که کوتاهترین مسیر تخمین راس "S" کمترین است.
• لبه های خروجی راس "S" آرام هستند.

قبل از آرامش لبه-

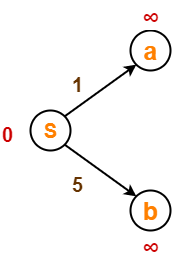
اکنون،

• d [S] + 1 = 0 + 1 = 1 <∞

∴ d [a] = 1 و Π [a] = S

• d [S] + 5 = 0 + 5 = 5 <∞

∴ d [b] = 5 و Π [b] = S

بعد از آرامش لبه ، درخت کوتاهترین مسیر ما

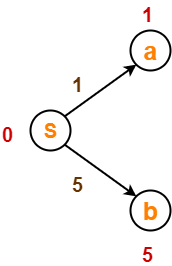
اکنون ، مجموعه ها به روز می شوند

• مجموعه بازدید نشده: {a، b، c، d، e}
• مجموعه بازدید شده: {S}

مرحله 04:

• راس "a" انتخاب شده است.
• این به این دلیل است که کوتاهترین مسیر تخمین راس "a" کمترین است.
• لبه های خروجی راس "a" آرام هستند.

قبل از آرامش لبه-

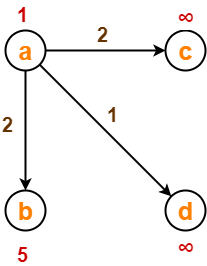
اکنون،

• d [a] + 2 = 1 + 2 = 3 <∞

∴ d [c] = 3 و Π [c] = a

• d [a] + 1 = 1 + 1 = 2 <∞

∴ d [d] = 2 و Π [d] = a

• d [b] + 2 = 1 + 2 = 3 <5

∴ d [b] = 3 و Π [b] = a

بعد از آرامش لبه ، درخت کوتاهترین مسیر ما

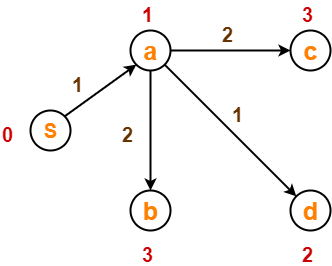
اکنون ، مجموعه ها به روز می شوند

• مجموعه بازدید نشده: {b، c، d، e}
• مجموعه بازدید شده: {S، a}

مرحله 05:

• Vertex 'd' انتخاب شده است.
• این بدان دلیل است که کوتاهترین مسیر تخمین برای راس "d" کمترین است.
• لبه های خروجی راس "d" آرام هستند.

قبل از آرامش لبه-

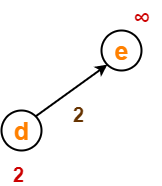
اکنون،

• d [d] + 2 = 2 + 2 = 4 <∞

∴ d [e] = 4 و Π [e] = d

بعد از آرامش لبه ، درخت کوتاهترین مسیر ما

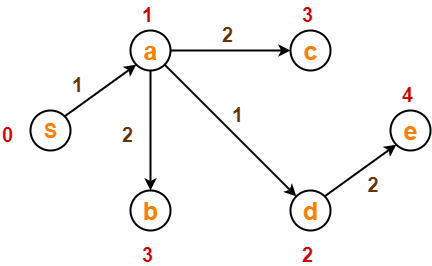
اکنون ، مجموعه ها به روز می شوند

• مجموعه بازدید نشده: {b، c، e}
• مجموعه بازدید شده: {S، a، d}

مرحله 06:

• راس "b" انتخاب شده است.
• دلیل این امر این است که کوتاهترین مسیر تخمین راس "b" کمترین است.
• راس 'c' نیز ممکن است انتخاب شود زیرا برای هر دو رئوس ، کوتاهترین برآورد مسیر کمترین است.
• لبه های خروجی راس "b" آرام هستند.

قبل از آرامش لبه-

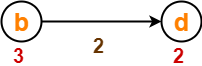
اکنون،

• d [b] + 2 = 3 + 2 = 5> 2

∴ بدون تغییر

پس از آرامش لبه ، درخت کوتاه ترین مسیر ما همانند مرحله 05 باقی می ماند.

اکنون ، مجموعه ها به روز می شوند

• مجموعه بازدید نشده: {c ، e}
• مجموعه بازدید شده: {S، a، d، b}

مرحله 07:

• Vertex 'c' انتخاب شده است.
• این بدان دلیل است که کوتاهترین مسیر تخمین برای راس 'c' کمترین است.
• لبه های خروجی راس "c" آرام هستند.

قبل از آرامش لبه-

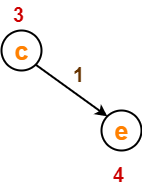
اکنون،

• d [c] + 1 = 3 + 1 = 4 = 4

∴ بدون تغییر

پس از آرامش لبه ، درخت کوتاه ترین مسیر ما همانند مرحله 05 باقی می ماند.

اکنون ، مجموعه ها به روز می شوند

• مجموعه بازدید نشده: {e}
• مجموعه بازدید شده: {S، a، d، b، c}

مرحله 08:

• راس 'e' انتخاب شده است.
• این بدان دلیل است که کوتاهترین برآورد مسیر برای راس 'e' کمترین است.
• لبه های خروجی راس 'e' آرام هستند.
• هیچ لبه خروجی برای راس "e" وجود ندارد.
• بنابراین ، درخت کوتاه ترین مسیر ما همانند مرحله 05 باقی مانده است.

اکنون ، مجموعه ها به روز می شوند

• مجموعه بازدید نشده: {}
• مجموعه بازدید شده: {S، a، d، b، c، e}

اکنون،

• تمام رئوس نمودار پردازش می شوند.
• درخت کوتاه ترین مسیر نهایی ما به شرح زیر است.
• این نشان دهنده کوتاهترین مسیر از راس منبع 'S' تا سایر رئوس باقی مانده است.

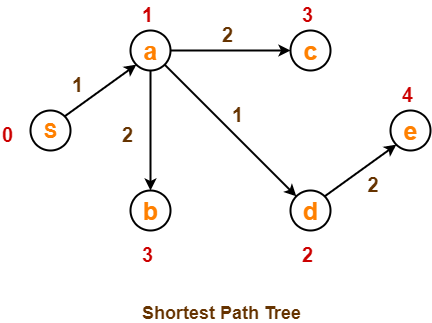
ترتیب پردازش تمام رئوس به ترتیب زیر است:

S ، a ، d ، b ، c ، e .

https://www.gatevidyalay.com/tag/dijkstras-algorithm-table/