ادامه دنباله دقیق

توسط علی رضا نقش نیلچی | چهارشنبه دوازدهم آذر ۱۳۹۹ | 20:9

گراد ، حلقه و تقسیم در هندسه دیفرانسیل [ ویرایش ]

این بخش ممکن است برای مطابقت با استانداردهای کیفیت ویکی پدیا نیاز به پاکسازی داشته باشد . مشکل خاص این است: استفاده زیاد از "ما" ، "یادداشت". همچنین ، این بخش برای اکثر خوانندگان این مقاله بیش از حد فنی است: باید آن را به تعاریفی که برای درک گزاره (دقت یک توالی) لازم است ، تقلیل داد. اثبات و جزئیات فنی متعلق به این مقاله نیستند ، اما باید در مقاله هندسه دیفرانسیل موجود باشد. اگر می توانید لطفاً در بهبود این بخش کمک کنید. ( دسامبر 2019 ) (با نحوه و زمان حذف این پیام الگو آشنا شوید )

مثال دیگر را می توان از هندسه دیفرانسیل ، به ویژه مربوط به کار در معادلات ماکسول ، استخراج کرد .

فضای هیلبرت را در نظر بگیرید $L ^ {2}$ توابع مجذور مربع با ارزش مقیاسی در سه بعد - سایپرز ، باشگاه دانش ${\ displaystyle \ left \ lbrace f: \ mathbb {R} ^ {3} \ to \ mathbb {R} \ right \ rbrace}$ . گرفتن شیب یک تابع ${\ displaystyle f \ in \ mathbb {H} _ {1}}$ ما را به زیرمجموعه ای از ${\ displaystyle \ mathbb {H} _ {3}}$ ، فضای توابع ارزش پذیر ، هنوز هم مجتمع با مربع در یک دامنه ${\ displaystyle \ left \ lbrace f: \ mathbb {R} ^ {3} \ to \ mathbb {R} ^ {3} \ right \ rbrace}$ - به طور خاص ، مجموعه ای از این توابع که نشان دهنده زمینه های بردار محافظه کار هستند. ( قضیه کلی استوکس یکپارچگی را حفظ کرده است.)

اول ، توجه داشته باشید که حلقه این قسمتها صفر است - از آن زمان

${\ displaystyle {\ start {تراز شده} \ operatorname {curl} (\ operatorname {grad} f) و \ Equ \ nabla \ بار (\ nabla f) = 0 \ پایان {تراز شده}}}$

برای همه چنین f . با این حال ، این فقط اثبات می کند که تصویر شیب زیر مجموعه هسته حلقه است. برای اثبات اینکه آنها در واقع همان مجموعه هستند ، عکس این را ثابت کنید: اگر حلقه یک قسمت برداری باشد ${\ vec {F}}$ است ، پس ${\ vec {F}}$ شیب برخی از عملکردهای اسکالر است. این تقریباً بلافاصله از قضیه استوکس دنبال می شود (به اثبات نیروی محافظه کار مراجعه کنید .) تصویر گرادیان دقیقاً هسته حلقه است و بنابراین می توانیم حلقه را شکل بعدی خود قرار دهیم ، و ما را دوباره به یک (متفاوت) زیر مجموعه ${\ displaystyle \ mathbb {H} _ {3}}$ .

به طور مشابه ، ما توجه داریم که

${\ displaystyle {\ start {تراز شده} \ operatorname {div} (\ operatorname {curl} {\ vec {v}}) و \ Equ \ nabla \ cdot \ nabla \ times {\ vec {v}} = 0 ، \ پایان {تراز شده}}}$

بنابراین تصویر حلقه فرعی است از هسته واگرایی . گفتگو تا حدودی درگیر است:

نشان دادناثبات آن ${\ displaystyle \ operatorname {div} {\ vec {F}}}$ = 0 دلالت دارد ${\ displaystyle {\ vec {F}} = \ operatorname {curl} {\ vec {A}}}$ برای بعضی ها ${\ vec {A}}$

پس از اثبات اینکه تصویر حلقه دقیقاً هسته واگرایی است ، این شکل گیری به نوبه خود ما را به فضایی که از آن شروع کرده ایم برمی گرداند. $L ^ {2}$ . از آنجا که به طور تعریف شده ما در فضایی از توابع قابل ادغام قرار گرفته ایم ، هر نوع عملکردی می تواند (حداقل به طور رسمی) به منظور تولید یک قسمت برداری که واگرایی همان عملکرد است - یکپارچه شود ، بنابراین تصویر واگرایی تمامیت $L ^ {2}$ ، و می توانیم توالی خود را تکمیل کنیم:

${\ displaystyle 0 \ به L ^ {2} \؛ \؛ {\ xrightarrow {\ operatorname {grad}}} \؛ \؛ \ mathbb {H} _ {3} \؛ \؛ {\ xrightarrow {\ operatorname { curl}}} \؛ \؛ \ mathbb {H} _ {3} \؛ \؛ {\ xrightarrow {\ operatorname {div}}} \؛ \؛ L ^ {2} \ به 0}$

معادل آن ، ما می توانستیم برعکس استدلال کنیم: در یک فضای متصل به سادگی ، یک قسمت برداری بدون پیچ و خم (یک قسمت در هسته حلقه) همیشه می تواند به عنوان یک شیب از یک تابع مقیاسی نوشته شود (و بنابراین در تصویر شیب) به همین ترتیب ، یک قسمت واگرایی را می توان به صورت حلقه ای از فیلد دیگر نوشت. [1] (بنابراین استدلال در این جهت از این واقعیت استفاده می کند که فضای 3 بعدی از نظر توپولوژیکی پیش پا افتاده است).

این دنباله دقیق کوتاه همچنین می تواند اثبات بسیار کوتاه تری از اعتبار تجزیه هلمولتز را که به حساب بردار نیروی بی رحم متکی نیست ، فراهم کند. دنباله را در نظر بگیرید

${\ displaystyle 0 \ به L ^ {2} \؛ \؛ {\ xrightarrow {\ operatorname {grad}}} \؛ \؛ \ mathbb {H} _ {3} \؛ \؛ {\ xrightarrow {\ operatorname { curl}}} \؛ \؛ \ operatorname {im} (\ operatorname {curl}) \ تا 0.}$

از آنجا که واگرایی شیب لاپلاکی است ، و از آنجا که فضای هیلبرت از توابع مربع مجتمع را می توان توسط توابع ویژه Laplacian گسترش داد ، در حال حاضر می بینیم که برخی از نقشه های معکوس ${\ displaystyle \ nabla ^ {- 1}: \ mathbb {H} _ {3} \ به L ^ {2}}$ باید وجود داشته باشد برای ساخت واضح چنین معکوس ، می توانیم از تعریف بردار لاپلاس شروع کنیم

${\ displaystyle \ nabla ^ {2} {\ vec {A}} = \ nabla (\ nabla \ cdot {\ vec {A}}) + \ nabla \ times (\ nabla \ times {\ vec {A}}) }$

از آنجایی که ما در تلاش هستیم تا با ترکیب برخی از عملکردها با شیب ، یک نقشه برداری هویتی ایجاد کنیم ، این را در مورد خود می دانیم ${\ displaystyle \ nabla \ times {\ vec {A}} = \ operatorname {curl} ({\ vec {A}}) = 0}$ . پس اگر واگرایی هر دو طرف را در نظر بگیریم

${\ displaystyle {\ start {تراز شده} \ nabla \ cdot \ nabla ^ {2} {\ vec {A}} & = \ nabla \ cdot \ nabla (\ nabla \ cdot {\ vec {A}}) \\ & = \ nabla ^ {2} (\ nabla \ cdot {\ vec {A}}) \\\ پایان {تراز شده}}}$

می بینیم که اگر یک تابع یک عملکرد ویژه بردار Laplacian باشد ، واگرایی آن باید یک عملکرد ویژه Laplacian مقیاس با همان مقدار ویژه باشد. سپس می توانیم عملکرد معکوس خود را بسازیم ${\ displaystyle \ nabla ^ {- 1}}$ به سادگی با شکستن هر عملکردی در ${\ displaystyle \ mathbb {H} _ {3}}$ به مبنای ویژه بردار-لاپلاس ، مقیاس گذاری هر یک با معکوس ارزش ویژه آنها و گرفتن واگرایی ؛ عمل از ${\ displaystyle \ nabla ^ {- 1} \ circ \ nabla}$ بنابراین به وضوح هویت است. بنابراین با تقسیم لما ،

${\ displaystyle \ mathbb {H} _ {3} \ Cong L ^ {2} \ oplus \ operatorname {im} (\ operatorname {curl})}$ ،

یا به طور معادل ، هر یک از قسمت های برداری مجذور مربع در $\ mathbb {R} ^ {3}$ می تواند به جمع یک گرادیان و یک حلقه شکسته شود - چیزی که ما برای اثبات آن تلاش کردیم.

خصوصیات [ ویرایش ]

لم تقسیم می گوید که اگر دنباله دقیقکوتاه

${\ displaystyle 0 \ به A \؛ {\ xrightarrow {\ f \}} \؛ B \؛ {\ xrightarrow {\ g \}} \؛ C \ به 0}$

اذعان morphism تی : B → به طوری که تی ∘ F هویت است یا morphism تو : C → B به طوری که گرم ∘ تو هویت است C ، پس از آن B است مجموع مستقیم از و C (برای غیر - گروههای جایگزین ، این یک محصول نیمه مستقیم است ). یکی می گوید که چنین توالی دقیق کوتاهی تقسیم می شود .

مار لم نشان می دهد که چگونه یک نمودار جابجایی با دو ردیف دقیق افزایش می دهد به یک توالی طولانی تر دقیق. نه لم یک مورد خاص است.

پنج لم شرایطی که تحت آن نقشه وسط در یک نمودار جابجایی با ردیف دقیق طول 5 ریخت است می دهد. کوتاه پنج لم یک مورد خاص آن استفاده به توالی دقیق کوتاه است.

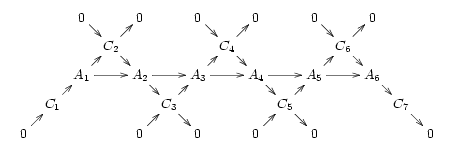
اهمیت توالی دقیق کوتاه با این واقعیت تأکید می شود که هر دنباله دقیق از "بافتن با هم" چندین توالی دقیق کوتاه همپوشانی ناشی می شود. به عنوان مثال توالی دقیق را در نظر بگیرید

$A_ {1} \ به A_ {2} \ به A_ {3} \ به A_ {4} \ به A_ {5} \ به A_ {6}$

که به معنای وجود اشیا C Ck در گروه است به گونه ای که

$C_ {k} \ Cong \ ker (A_ {k} \ به A_ {k + 1}) \ Cong \ operatorname {im} (A_ {k-1} \ به A_ {k})$ .

علاوه بر این فرض کنید هسته هسته هر مورفیسم وجود داشته باشد و با تصویر مورفیسم بعدی در دنباله یکدست باشد:

$C_ {k} \ Cong \ operatorname {coker} (A_ {k-2} \ به A_ {k-1})$

(این برای تعدادی از دسته های جالب ، از جمله هر دسته از آبلیان مانند گروه های آبلی ، درست است ؛ اما برای همه دسته هایی که توالی دقیق را مجاز می دانند ، درست نیست ، و به ویژه برای گروهی که در آنها کوکر وجود دارد ، درست نیست) ج ): G → H است H / IM ( F ) اما $H / {\ left \ langle \ operatorname {im} f \ right \ rangle} ^ {H}$ ، ضریب H با بسته شدن مزدوج im ( f ).) سپس یک نمودار جابجایی بدست می آوریم که در آن تمام موربها توالی دقیق کوتاه هستند:

تنها بخشی از این نمودار که به شرایط کوکرنل بستگی دارد ، جسم است ${\ textstyle C_ {7}}$ و جفت نهایی شکل گیری ها ${\ textstyle A_ {6} \ به C_ {7} \ به 0}$ . در صورت وجود هر شی $A _ {{k + 1}}$ و مورفيسم ${\ displaystyle A_ {k} \ به A_ {k + 1}}$ به طوری که ${\ displaystyle A_ {k-1} \ به A_ {k} \ به A_ {k + 1}}$ دقیق است ، سپس دقیق بودن ${\ displaystyle 0 \ به C_ {k} \ به A_ {k} \ به C_ {k + 1} \ به 0}$ اطمینان حاصل می شود باز هم با مثال گرفتن از دسته گروه ها ، این واقعیت که( im ( fهسته برخی از همگونی ها در H است ، به این معنی است که یک زیر گروه عادی است ، که همزمان با بسته شدن مزدوج آن است. بنابراین کوکر ( f ) با تصویر( H / im ( f مورفیسم بعدی یکدست است.

برعکس ، با توجه به هر لیستی از توالی های کوتاه کوتاه همپوشانی ، اصطلاحات میانی آنها یک توالی دقیق را به همان شیوه تشکیل می دهند.

کاربردهای دنباله دقیق [ ویرایش ]

در تئوری مقوله های آبلیان ، توالی های دقیق کوتاه اغلب به عنوان یک زبان مناسب برای صحبت در مورد اشیا sub زیر و فاکتور استفاده می شود.

مشکل پسوند است که در اصل این پرسش که "با توجه به شرایط پایان و C از یک توالی دقیق کوتاه، چه احتمالات را برای حد وسط وجود داشته باشد ب ؟" در گروه گروه ها ، این معادل این س ،ال است که چه گروه های B دارای A به عنوان یک زیر گروه نرمال و C به عنوان گروه عامل مربوطه هستند؟ این مسئله در طبقه بندی گروه ها مهم است . همچنین به گروه اتومورفیسم بیرونی مراجعه کنید .

توجه داشته باشید که در دنباله دقیق، ترکیب F من 1 ∘ F من نقشه من به 0 در من 2 ، بنابراین هر توالی دقیق است زنجیره ای پیچیده . علاوه بر این، تنها F من تصاویر از عناصر من به 0 توسط نقشه برداری F من 1 ، به طوری که همسانی این مجموعه زنجیره ای بی اهمیت است. به طور خلاصه تر:

توالی دقیق دقیقاً آن مجموعه های زنجیره ای است که حلقوی هستند .

با توجه به هر مجموعه پیچیده ای ، بنابراین می توان همسانی آن را معیاری برای اندازه گیری دقیق بودن آن دانست.

اگر یک سری دنباله دقیق کوتاه به هم پیوسته توسط مجتمع های زنجیره ای (یعنی یک توالی دقیق کوتاه از مجتمع های زنجیره ای یا از دیدگاه دیگر ، یک مجموعه زنجیره ای از توالی های دقیق کوتاه) را بدست آوریم ، پس می توانیم از این امر دقیقاً طولانی مدت بدست آوریم توالی (یعنی یک توالی دقیق که توسط اعداد طبیعی نمایه می شود) در همسانی با استفاده از لامای زیگ زاگ . این در توپولوژی جبری در مطالعه همسانی نسبی مطرح می شود .دنباله مایر Vietoris مثال دیگری است. توالی دقیق طولانی که توسط دنباله دقیق کوتاه ایجاد می شود نیز از ویژگی های عامل های مشتق شده است .

functors دقیق هستند functors که تبدیل دنباله دقیق را به دنباله دقیق.

منابع

https://en.wikipedia.org/wiki/Exact_sequence

مشخصات وب

در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
09132003030

ریاضیات

آموزش ریاضی