لم مار یک ابزار مورد استفاده در است ریاضیات ، به ویژه جبر همسان ، برای ساخت دنباله طولانی دقیق . لمام مار در هر گروه آبلی معتبر است و ابزاری اساسی در جبر همولوژی و کاربردهای آن است ، به عنوان مثال در توپولوژی جبری . همومرفیسم هاي ساخته شده با كمك آن را بطور معمول همومرفیسم هاي اتصال دهنده مي نامند .
فهرست
بیانیه [ ویرایش ]
در یک دسته آبلی (مانند دسته گروههای آبلی یا دسته فضاهای برداری در یک زمینه مشخص ) ، یک نمودار جابجایی در نظر بگیرید :
که در آن ردیف ها دنباله دقیق هستند و 0 شی صفر است .
سپس دنباله دقیق مربوط وجود دارد دانه و هم هسته از ، ب ، و ج :
جایی که d یک همریختی است ، معروف به هومومورفیسم اتصال دهنده است .
به علاوه، اگر همریختی F است تکریختی ، پس از آن به طوری که همریختی است
هسته های موجود در اینجا عبارتند از:
توضیح نام [ ویرایش ]
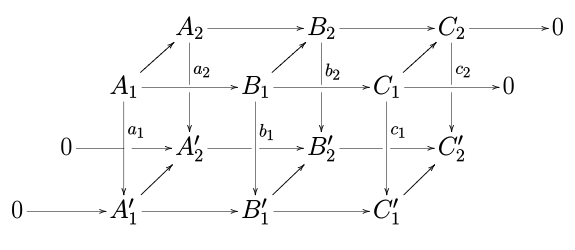
برای دیدن نام لماس مار از کجا نامگذاری شده است ، نمودار بالا را به شرح زیر گسترش دهید:
و سپس توجه داشته باشید که دنباله دقیق که نتیجه لما است را می توان بر روی این نمودار گسترش یافته در شکل معکوس "S" یک مار لغزنده ترسیم کرد .
ساخت نگاشت ها [ ویرایش ]
نگاشت های بین هسته ها و نگاشت های بین هسته ها به دلیل طبیعی بودن نمودار توسط نگاشت های داده شده (افقی) به صورت طبیعی القا می شوند. صحت دو دنباله القایی به طور مستقیم از صحت ردیف های نمودار اصلی پیروی می کند. بیانات مهم لم است که یک همریخت اتصال د وجود دارد که کامل دنباله دقیق.
در مورد گروه ها یا مدول ها های آبلی بیش از برخی حلقه ها ، می توان نگاشت d را به صورت زیر ساخت:
یک عنصر x را در ker c انتخاب کنید و آن را به عنوان عنصر C مشاهده کنید . از g است پوشا وجود دارد، Y در B با g ( Y ) = X . به دلیل اشتراکی نمودار ، ما باید g ' ( b ( y )) = c ( g ( y )) = c ( x ) = 0 (از آنجا که x در هسته c است ) ، و بنابراین b ( y ) در هسته استG ' . از آنجا که ردیف پایین دقیق است ، یک عنصر z را در A ' با f ' ( z ) = b ( y ) پیدا می کنیم. z با تزریق f ' منحصر به فرد است . سپس d ( x ) = z + im ( a ) را تعریف می کنیم . حال باید بررسی شود که d کاملاً تعریف شده باشد (یعنی d ( x ) فقط به x بستگی دارد نه به انتخاب y) ، این یک همریختی است و دنباله طولانی حاصل از آن واقعاً دقیق است. به طور مرتب می توان با تعقیب نمودار صحت را بررسی کرد (به اثبات لم 9.1 در [1] مراجعه کنید ).
هنگامی که این کار انجام شد ، قضیه برای گروه ها یا مدول ها های آبلی بیش از یک حلقه ثابت می شود. برای حالت کلی ، ممکن است استدلال از نظر خصوصیات پیکان ها و لغو به جای عناصر ، دوباره بیان شود. متناوباً ، ممکن است قضیه جاسازی میچل را استناد کند .
طبیعی بودن [ ویرایش ]
در برنامه ها ، اغلب لازم است نشان داده شود که دنباله های دقیق طولانی "طبیعی" هستند (به معنای تحولات طبیعی ). این از طبیعی بودن دنباله تولید شده توسط لم مار ناشی می شود.
اگر
یک نمودار جابجایی با دنباله دقیق است ، سپس لم مار را می توان دو بار ، به "جلو" و "پشت" اعمال کرد ، و دارای دو دنباله دقیق است. اینها با یک نمودار جابجایی از فرم مرتبط هستند
مثال [ ویرایش ]
فرض کنید 
![k[t]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd5ada407273702e537635ee01fb7c76c8ea78d8)
![{\displaystyle V\otimes _{k[t]}k=V\otimes _{k[t]}(k[t]/(t))=V/tV=\operatorname {coker} (t).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9658fc4d006085a13d0079fc13f503a0cb61a649)
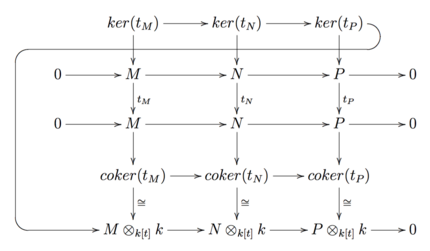
با توجه به یک دنباله دقیق کوتاه از 
![{\displaystyle M\otimes _{k[t]}k\to N\otimes _{k[t]}k\to P\otimes _{k[t]}k\to 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c668ecea8dbadb3e335a2c3b31975892847c9346)
![{\displaystyle 0\to M\otimes _{k[t]}k\to N\otimes _{k[t]}k\to P\otimes _{k[t]}k\to 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9949b000b55ce5b652d09861563b4c9e5c9225c6)
با توجه به نمودار بالا، می توانیم یک دنباله دقیق را القا کنیم ![{\displaystyle \ker(t_{M})\to \ker(t_{N})\to \ker(t_{P})\to M\otimes _{k[t]}k\to N\otimes _ {k[t]}k\to P\times _{k[t]}k\to 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcc63f9c13e761f3822a2df77c431a933751ab92)
در فرهنگ عامه [ ویرایش ]
اثبات لمای مار توسط شخصیت جیل کلایبورگ در همان ابتدای فیلم نوبتI در سال 1980 آموزش داده شده است . [2]
منبع
https://en.wikipedia.org/wiki/Snake_لم
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.