در ریاضیات ، به ویژه جبر همسان و کاربردهای دیگر از رسته آبلی تئوری، پنج لم مهم و به طور گسترده ای استفاده می شود لم در مورد نمودار جابجایی . پنج لم است که نه تنها برای رسته آبلی معتبر بلکه در کار رسته از گروه ، برای مثال.
می توان پنج لم را ترکیبی از دو قضیه دیگر تصور کرد ، چهار لم که با یکدیگر دوگانه هستند .
فهرست
بیانیه ها [ ویرایش ]
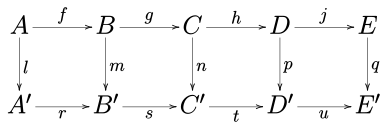
نمودار جابجایی زیر را در هر گروه آبلی (مانند رسته گروههای آبلی یا رسته فضاهای برداری در یک زمینه مشخص ) یا در گروه ها در نظر بگیرید.
پنج کشور لم که اگر ردیف هستند دقیق ، متر و ص هستند یکریختی ها ، L یک IS برو ریختی و Q است تکریختی ، و سپس N نیز یک ریخت.
دو حالت چهار لمی:
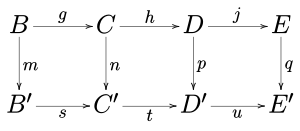
(1) اگر ردیفهای نمودار جابجایی باشد
دقیق هستند و m و p بروریختی هستند و q یک شکل است ، سپس n یک بروریختی است.
(2) اگر ردیف های نمودار جابجایی باشد
دقیق هستند و m و p یک شکل هستند و l یک بروریختی است ، سپس n یک شکل است.
اثبات [ ویرایش ]
روش اثبات ما استفاده می شود معمولا به عنوان تعقیب نمودار . [1] ما پنج لمی را با اثبات جداگانه هر یک از دو چهار لمی اثبات خواهیم کرد.
برای انجام تعقیب نمودار، ما فرض کنیم که ما در این رده هستند مدول بیش از برخی از حلقه ، به طوری که ممکن است ما از صحبت عناصر از اشیاء در نمودار و از همریختی ها از نمودار به عنوان فکر می کنم توابع (در واقع، همو مرفیسم ها ) اقدام در آن عناصر. سپس یک همریختی تکریختی است اگر و تنها اگر آن است تزریقی ، و آن را یک برو ریختی است اگر و تنها اگر آن را پوشا . به همین ترتیب ، برای مقابله با دقت ، می توانیم به هسته ها و تصاویر به معنای تئوری کارکرد بیندیشیم . دلیل این امر همچنان در مورد هر رسته (کوچک) آبلی اعمال خواهد شد قضیه تعبیه میچل ، که بیان می کند هر رسته کوچک آبلی را می توان به عنوان یک رسته از مدول ها بر روی برخی از حلقه ها نشان داد. برای گروه ها ، کافیست تمام علامت های افزودنی زیر را به علامت ضرب تبدیل کنید ، و توجه داشته باشید که از عواملی که از گروه آبلی استفاده می شود هرگز استفاده نمی شود
بنابراین ، برای اثبات (1) ، فرض کنید که m و p اضافی هستند و q قابل تزریق است.
اثبات (1) در مواردی که 
اثبات (1) در مواردی که 
- بگذارید c یک عنصری از C باشد .
- از آنجا که p اضافی است ، یک عنصر d در D با p ( d ) = t ( c ′ ) وجود دارد.
- با اشتراك نمودار ، u ( p ( d )) = q ( j ( d)).
- از آنجا که im t = ker u توسط دقت ،(( 0 = u ( t ( c ′ )) = u ( p ( d )) = q ( j ( d .
- از آنجا که q قابل تزریق است ، j ( d ) = 0 ، بنابراین d در ker j = im h است .
- بنابراین ، c در C با h ( c ) = d وجود دارد .
- سپس t ( n ( c )) = p ( h ( c )) = t ( c ′ ). از آنجا که t یک همگونی است ، از این رو t ( c ′ - n ( c )) = 0 نتیجه می گیرد.
- به طور دقیق ، c ′ - n ( c ) در تصویر s است ، بنابراین b ′ در B ′ با s ( b ′ ) = c ′ - n ( c ) وجود دارد.
- از آنجا که m اضافی است ، بنابراین می توانیم b را در B پیدا کنیم به طوری که b ′ = m ( b ).
- با اشتراك ، n ( g ( b )) = s ( m ( b )) = c ′ - n ( c ).
- از آنجا که n یکدست است ، n ( g ( b ) + c ) = n ( g ( b )) + n ( c ) = c ′ - n ( c ) + n ( c ) = c .
- بنابراین ، n صحیحی است.
سپس ، برای اثبات (2) ، فرض کنید m و p تأثیرگذار و l اضافی است.
اثبات (2).
- بگذارید c در C به گونه ای باشد که n ( c ) = 0 باشد.
- t ( n ( c )) سپس 0 است.
- با اشتراك ، p ( h ( c )) = 0.
- از آنجا که p آمپول است ، h ( c ) = 0.
- به طور دقیق ، یک عنصر b از B وجود دارد به طوری که g ( b ) = c .
- با اشتراك ، s ( m ( b )) = n ( g ( b )) = n ( c ) = 0.
- به طور دقیق ، یک عنصر a ′ از A ′ وجود دارد به طوری که r ( a ′ ) = m ( b ).
- از آنجا که l صحیحی است ، a در A وجود دارد به طوری که l ( a ) = a ′ .
- با اشتقاق ، m ( f ( a )) = r ( l ( a )) = m ( b ) .
- از آنجا که m قابل تزریق است ، f ( a ) = b .
- بنابراین c = g ( f ( a )).
- از آنجا که ترکیب g و f بی اهمیت است ، c = 0.
- بنابراین ، n قابل تزریق است.
ترکیب دو چهار لمام اکنون پنج لم le کامل را اثبات می کند.
برنامه ها [ ویرایش ]
پنج لما اغلب در دنباله های دقیق طولانی اعمال می شود : هنگام محاسبه همسانی یا کوهومولوژی یک شی داده شده خاص ، یکی معمولاً از یک زیرشاخه ساده تر استفاده می کند که همسانی / کوهومولوژی آن مشخص است و به یک دنباله دقیق طولانی می رسد که شامل گروه های همسانی ناشناخته اصلی است. هدف - شی. این به تنهایی اغلب برای تعیین گروههای همسانی ناشناخته کافی نیست ، اما اگر بتوان از طریق مورفیسم شی شئ و زیر شی شئ اصلی را با موارد کاملاً خوب مقایسه کرد ، در این صورت مورفیسم بین دنباله دقیق طولانی مربوطه ایجاد می شود و پنج لما می توانند پس از آن برای تعیین گروههای همسانی ناشناخته استفاده می شود.
منبع
https://en.wikipedia.org/wiki/Five_lemma
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.