ریاضیات

مثالهای انگیزشی [ ویرایش ]

مناطق موجود در هواپیما [ ویرایش ]

مساحت یک متوازی الاضلاع از نظر تعیین کننده ماتریس مختصات دو راس آن است.

هواپیما دکارتی R 2 یک واقعی فضای برداری مجهز به یک پایه و اساس متشکل از یک جفت از بردار واحد

فرض کنید که

یک جفت بردار داده شده در R 2 هستند که در اجزا components نوشته شده اند. است یک متوازی الاضلاع داشتن منحصر به فرد وجود دارد V و W به عنوان دو طرف آن است. منطقه از این متوازی الاضلاع توسط استاندارد داده تعیین فرمول:

اکنون محصول خارجی v و w را در نظر بگیرید :

جایی که در مرحله اول از قانون توزیع کالا خارجی استفاده می شود و در مرحله آخر از این واقعیت استفاده می شود که محصول خارجی متناوب است و به ویژه e 2 ∧ e 1 = - ( e 1 ∧ e 2 ) . (این که محصول خارجی متناوب است نیز نیرو می گیرد.) توجه داشته باشید که ضریب در این عبارت آخر دقیقاً تعیین کننده ماتریس [ v w ] است . این واقعیت که این ممکن است مثبت یا منفی باشد ، این معنی شهودی را دارد که v و w ممکن است در جهت خلاف جهت عقربه های ساعت یا جهت عقربه های ساعت به عنوان راس های موازی که تعریف می کنند ، جهت گیری شوند. به چنین منطقه ای ناحیه امضا شده از متوازی الاضلاع گفته می شود: مقدار مطلق ناحیه امضا شده منطقه عادی است و علامت جهت گیری آن را تعیین می کند.

این واقعیت که این ضریب مساحت امضا شده است ، تصادفی نیست. در حقیقت ، اگر کسی بخواهد این ناحیه را به عنوان یک سازه جبری بدیهی کند ، می توان فهمید که محصول خارجی باید مربوط به ناحیه امضا شده باشد. به طور جزئی ، اگر A ( v ، w ) نشانگر ناحیه امضا شده از متوازی الاضلاع باشد که جفت بردارهای v و w دو ضلع مجاور را تشکیل می دهند ، A باید ویژگی های زیر را برآورده کند:

1. A ( r v ، s w ) = rs A ( v ، w ) برای هر عدد واقعی r و s ، از آنجا که رسوب دادن هر یک از دو طرف مساحت را به همان مقدار تغییر می دهد (و تغییر جهت یکی از طرفین جهت را معکوس می کند) از متوازی الاضلاع).
2. A ( v ، v ) = 0 ، از آنجا که مساحت متوازی الاضلاع منحط تعیین شده توسط v (یعنی یک بخش خط ) صفر است.
3. A ( w ، v ) = −A ( v ، w ) ، زیرا جایگزینی نقش های v و w جهت گیری موازی را معکوس می کند.
4. A ( v + r w ، w ) = A ( v ، w ) برای هر عدد واقعی r ، از آنجا که افزودن مضربی از w به v نه بر پایه و نه بر ارتفاع موازی تأثیر نمی گذارد و در نتیجه مساحت آن را حفظ می کند.
5. A ( e 1 ، e 2 ) = 1 ، زیرا مساحت مربع واحد یک است.

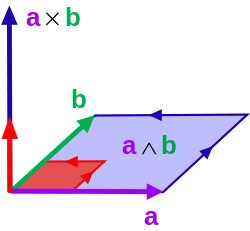
محصول متقاطع ( بردار آبی ) در رابطه با محصول خارجی ( متوازی الاضلاع آبی روشن ). طول محصول ضربدری به طول بردار واحد موازی ( قرمز ) است همانطور که اندازه محصول خارجی به اندازه موازی مرجع ( قرمز روشن ) است.

به استثنای آخرین ویژگی ، محصول خارجی دو بردار همان خصوصیات منطقه را برآورده می کند. به یک معنا خاص ، محصول خارجی ویژگی نهایی را تعمیم می دهد با اجازه دادن به مساحت یک متوازی الاضلاع با هر یک از متوازی الاگامهای "استاندارد" انتخاب شده در یک صفحه موازی (در اینجا یکی با اضلاع e 1 و e 2 ) مقایسه می شود. به عبارت دیگر ، محصول خارجی فرمولی مستقل از مبنا را ارائه می دهد. [6]

محصولات صلیبی و سه گانه [ ویرایش ]

برای بردارها در یک فضای برداری 3 بعدی گرا با یک محصول اسکالر دو خطی ، جبر خارجی ارتباط تنگاتنگی با محصول ضربدری و محصول سه گانه دارد . با استفاده از یک استاندارد استاندارد ( e 1 ، e 2 ، e 3 ) ، محصول خارجی یک جفت بردار

و

است

جایی که ( e 1 ∧ e 2 ، e 2 ∧ e 3 ، e 3 ∧ e 1 ) مبنایی برای فضای سه بعدی Λ 2 ( R 3 ) است. ضرایب فوق همان تعریف معمول محصول ضربدری بردارها در سه بعد با جهت معین است ، تنها تفاوت این است که محصول خارجی یک بردار معمولی نیست ، بلکه در عوض یک بردار 2 است و این محصول خارجی به انتخاب جهت بستگی ندارد.

آوردن بردار سوم

محصول خارجی سه بردار است

جایی که e 1 ∧ e 2 ∧ e 3 بردار اساس برای فضای یک بعدی Λ 3 ( R 3 ) است. ضریب اسکالر محصول سه گانه سه بردار است.

محصول ضربدری و محصول سه گانه در یک فضای بردار اقلیدسی سه بعدی هر یک تفسیرهای هندسی و جبری را پذیرفته است. محصول ضربدری u × v را می توان به عنوان بردار تفسیر کرد که عمود بر هر دو u و v باشد و اندازه آن برابر با مساحت متوازی الاضلاع تعیین شده توسط دو بردار باشد. همچنین می توان آن را به عنوان بردار متشکل از خردسالان ماتریس با ستونهای u و v تفسیر کرد . محصول سه گانه u ، v و  wیک اسکالر امضا شده است که یک حجم هندسی را نشان می دهد. از نظر جبری ، تعیین کننده ماتریس با ستونهای u ، v و  w است . محصول خارجی در سه بعد تفسیرهای مشابه را امکان پذیر می سازد: همچنین می توان آن را با خطوط جهت دار ، مناطق ، حجم ها و غیره شناسایی کرد که توسط یک ، دو یا چند بردار پوشانده شده اند. محصول خارجی این مفاهیم هندسی را به همه فضاهای برداری و به هر تعداد ابعادی تعمیم می دهد ، حتی در صورت عدم وجود محصول اسکالر.

منبع

https://en.wikipedia.org/wiki/Exterior_algebra