Tschirnhausen مکعب منحنی های جبری از درجه سه است.
در ریاضیات ، یک منحنی هواپیمای جبری وابسته ، مجموعه صفر یک چند جمله ای در دو متغیر است. منحنی صفحه جبری تصویری صفر مجموعه ای در یک است هواپیما تصویری از یک چند جمله ای همگن در سه متغیر. منحنی هواپیمای جبری آفیین با همگن کردن چند جمله ای تعریف کننده آن می تواند در یک منحنی هواپیمای جبری پروژکتور به پایان برسد . برعکس ، یک منحنی هواپیمای جبری پیش بینی شده از معادله همگن h ( x ، y ، t ) = 0 را می توان منحنی صفحه جبر عاطفی از معادله h محدود کرد( x ، y ، 1) = 0 . این دو عملیات هر دو با یکدیگر معکوس هستند. بنابراین ، عبارت منحنی هواپیمای جبری غالباً بدون مشخص کردن صریح اینکه آیا آن جنب است یا مورد پروژکی مورد نظر است ، بکار می رود.
به طور کلی ، یک منحنی جبری یک نوع جبری از ابعاد یک است. به طور برابر ، یک منحنی جبری یک نوع جبری است که از نظر بیداری معادل یک منحنی هواپیمای جبری است. اگر منحنی در یک فضای عاطفه یا یک فضای پروژکتور موجود باشد ، فرد می تواند یک پیش بینی چنین معادله ای را به خود بگیرد.
این معادلات دزدی دریایی بیشتر مطالعه منحنی های جبری را به مطالعه منحنی های هواپیمای جبری کاهش می دهد. با این حال ، برخی از خواص تحت معادل Biriation نگهداری نمی شوند و باید در منحنی های غیر هواپیما مورد مطالعه قرار گیرند. این به ویژه در مورد درجه و روان بودن صادق است . به عنوان مثال ، منحنی های صاف از جنس 0 و درجه بیشتر از دو وجود دارد ، اما هر پیش بینی هواپیما از این منحنی ها دارای نقاط یکتایی است (به فرمول درجه Genus مراجعه کنید ).
منحنی غیر هواپیما غالباً منحنی فضایی یا منحنی خمیده نامیده می شود .
فهرست
- 1در هندسه اقلیدسی
- 2منحنی های پروژکتور هواپیما
- 3نقاط قابل توجه منحنی هواپیما
- 4ساختار تحلیلی
- 5منحنی های جبری غیر هواپیما
- 6زمینه های عملکرد جبری
- 7منحنی های پیچیده و سطوح واقعی
- 8تکین ها
- 9نمونه هایی از منحنی ها
- 10همچنین ببینید
- 11یادداشت
- 12منابع
در هندسه اقلیدسی [ ویرایش ]
یک منحنی جبری در هواپیمای اقلیدسی مجموعه نقاطی است که مختصات آن ، راه حل های معادله چند جملهای دو متغیره p ( x ، y ) = 0. این معادله است که بر خلاف منحنی هایی که اغلب معادله ضمنی از منحنی نامیده می شود. نمودار عملکردی است که صریحاً y را به عنوان تابعی از x تعریف می کند .
با منحنی داده شده توسط چنین معادله ضمنی ، اولین مشکلات تعیین شکل منحنی و ترسیم آن است. این مشکلات به آسانی به عنوان در مورد نمودار یک تابع، که برای آن را حل نمی کند Y به راحتی ممکن است برای مقادیر مختلف محاسبه شود X . این واقعیت که معادله تعریف شده چند جمله ای است ، دلالت بر این دارد که منحنی دارای برخی خصوصیات ساختاری است که ممکن است در حل این مشکلات کمک کند.
هر منحنی جبری ممکن است به صورت منحصر به فرد به تعداد محدودی از قوسهای یکنواخت صاف (که شاخه ها نیز نامیده می شوند ) که گاهی توسط بعضی نقاط متصل می شوند که بعضاً "نقاط قابل توجه" نامیده می شوند ، و احتمالاً تعداد محدودی از نقاط جدا شده به نام آکنه ها وجود داشته باشد. قوس یکنواخت صاف نمودار یک است تابع صاف است که تعریف شده و یکنواخت بر روی یک فاصله باز از X محور. در هر جهت ، یک قوس یا بدون محدودیت (معمولاً به عنوان یک قوس نامتناهی گفته می شود ) یا دارای یک نقطه انتهایی است که یا یک نقطه مفرد است (این در زیر تعریف خواهد شد) یا یک نقطه با یک موانع مماس با یکی از محورهای مختصات.
به عنوان مثال ، برای مکعب Tschirnhausen ، دو قوس نامتناهی وجود دارد که منشاء آنها (0/0) از نقطه انتهایی است. این نقطه تنها نقطه منحصر به فرد منحنی است. همچنین دو قوس وجود دارد که از این نقطه منفرد به عنوان یک نقطه انتهایی و داشتن یک نقطه پایانی دوم با یک مماس افقی برخوردار هستند. سرانجام ، دو قوس دیگر وجود دارد که هر کدام یکی از این نقاط را با مماس افقی به عنوان نقطه انتهایی اول و داشتن نقطه منحصر به فرد با مماس عمودی به عنوان نقطه پایانی دوم قرار می دهند. در مقابل ، سینوسوئید مطمئناً منحنی جبری نیست و دارای تعداد نامتناهی قوس های یکتایی است.
برای ترسیم منحنی جبری ، شناختن نکات قابل توجه و مماس آنها ، شاخه های نامتناهی و مجانب آنها (در صورت وجود) و نحوه اتصال قوس ها به آنها بسیار مهم است. همچنین در نظر گرفتن نقاط تورم به عنوان نقاط قابل توجه مفید است. وقتی تمام این اطلاعات روی یک برگه کاغذ کشیده می شود ، شکل منحنی معمولاً کاملاً واضح به نظر می رسد. اگر اینگونه نباشد ، کافی است برای به دست آوردن توضیحی خوب از منحنی ، چند نکته دیگر و مماس آنها را اضافه کنیم.
روش های محاسبه نکات قابل توجه و مماس آنها پس از بخش منحنی های طرح دار در زیر توضیح داده شده است .
منبع
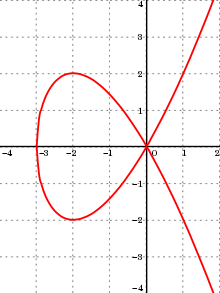
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.