در ریاضیات ، به ویژه هندسه جبری ، یک فضای مدولار یک فضای هندسی (معمولاً یک طرح یا یک پشته جبری ) است که نقاط آن نمایانگر اشیاء جبری از نوع ثابت یا کلاس های ایزومورفیسم از این قبیل اشیاء است. چنین فضاهایی اغلب به عنوان راه حل برای مشکلات طبقه بندی بوجود می آیند: اگر بتوان نشان داد که مجموعه ای از اشیاء جالب (به عنوان مثال ، منحنی های جبری صاف از یک جنس ثابت)) می توان به ساختار یک فضای هندسی داده شد ، سپس می توان با معرفی مختصات در فضای حاصل ، چنین اشیاء را پارامتر کرد. در این زمینه ، اصطلاح "modulus" مترادف با "پارامتر" استفاده می شود؛ فضاهای ماژول ابتدا به عنوان فضاهای پارامترها و نه به عنوان فضاهای اشیاء شناخته می شدند. نوع فضای ماژول ها مدول های رسمی هستند .
فهرست
- 1انگیزه
- 2مثالهای اساسی
- 3تعاریف
- 4مثالهای بعدی
- 5روش هایی برای ساخت فضاهای مدولار
- 6در فیزیک
- 7همچنین ببینید
- 8منابع
- 9لینک های خارجی
انگیزه [ ویرایش ]
فضاهای مدولار فضاهای راه حل مشکلات طبقه بندی هندسی هستند. یعنی نقاط یک فضای مدولار با راه حلهای مشکلات هندسی مطابقت دارد. در اینجا راه حلهای مختلف مشخص می شوند که ایزومورف باشند (یعنی از نظر هندسی یکسان هستند). می توان تصور کرد که فضاهای مدول به عنوان ایجاد فضای جهانی از پارامترها برای مشکل است. به عنوان مثال ، مشکل پیدا کردن همه حلقه های موجود در هواپیمای اقلیدسی را تا هماهنگی در نظر بگیرید. هر دایره ای را می توان با اختصاص سه امتیاز به صورت منحصر به فرد توصیف کرد ، اما بسیاری از مجموعه های مختلف از سه نقطه یک دایره یکسان را ارائه می دهند: مکاتبات بسیار به یک است. با این وجود ، دایره ها با دادن مرکز و شعاع خود به طور جداگانه پارامتر می شوند: این دو پارامتر واقعی و یک پارامتر واقعی مثبت است. از آنجا که ما فقط به محافل "تا هماهنگی" علاقه مندیم ، ما دایره هایی با مراکز مختلف اما شعاع یکسان را شناسایی می کنیم ، بنابراین شعاع به تنهایی برای پارامتر کردن مجموعه مورد علاقه کافی است. بنابراین فضای ماژول ها استاعداد حقیقی مثبت .
فضاهای مدول اغلب ساختارهای هندسی طبیعی و توپولوژیکی نیز دارند. به عنوان مثال ، در مثال حلقهها ، فضای ماژولها فقط یک مجموعه انتزاعی نیستند ، بلکه مقدار مطلق اختلاف شعاع برای تعیین زمان نزدیک بودن دو دایره یک متریک را تعیین می کند. ساختار هندسی فضاهای مدول به صورت محلی به ما می گوید دو راه حل از یک مسئله طبقه بندی هندسی "نزدیک" هستند ، اما به طور کلی فضاهای مدول نیز از یک ساختار جهانی پیچیده نیز برخوردار هستند.
ساخت P 1 ( R ) با تغییر 0 ≤ θ <π یا به عنوان فضای اختصاصی S 1 .
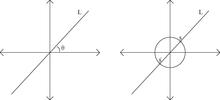
به عنوان مثال ، چگونگی توصیف مجموعه خطوط در R 2 را که از منشاء تقاطع دارند ، در نظر بگیرید. ما می خواهیم به هر خط L این خانواده مقداری اختصاص دهیم که بتواند آن را بطور جداگانه مشخص کند - یک مدول. مثالی از چنین مقدار ، زاویه مثبت θ ( L ) با رادیان 0 ≤ θ <π است. مجموعه خطوط L بنابراین پارامتر شده به عنوان P 1 ( R ) شناخته می شود و خط پروژکتور واقعی نامیده می شود .
همچنین می توان مجموعه خطوط موجود در R 2 را توصیف کرد که منشأ آن را با استفاده از یک ساختار توپولوژیکی تقاطع می کنند. به شوخ طبعی: نظر S 1 ⊂ R 2 و توجه کنید که هر نقطه بازدید کنندگان ∈ S 1 می دهد خط L ( بازدید کنندگان ) در مجموعه (که منشاء می پیوندد و ها ). با این حال، این نقشه دو به یک است، بنابراین ما می خواهید برای شناسایی بازدید کنندگان ~ - ها به عملکرد P 1 ( R ) ≅ S 1 / ~ که در آن توپولوژی در این فضا است توپولوژی بهره ناشی ازنقشه قطعی S 1 → P 1 ( R ).
بنابراین، هنگامی که ما در نظر P 1 ( R ) به عنوان یک فضای مدول از خطوط که از وسط قطع مبدا در R 2 ، ما راه که در آن اعضای خانواده (خطوط در این مورد) می توانید با تغییر پیوسته 0 ≤ θ <بم ضبط π
مثالهای اساسی [ ویرایش ]
فضای پروژه ای و Grassmannians [ ویرایش ]
واقعی تصویری فضای P N یک فضای مدول که parametrizes فضای خطوط در R N 1 که از مبدا منتقل می کند. به طور مشابه، فضا پیچیده تصویری فضای تمام خطوط پیچیده در C N 1 عبور از مبدا.
به طور کلی ، G Grassmannian G ( k ، V ) یک فضای بردار V بر روی یک میدان F ، فضای مدولار کلیه زیر فضاهای خطی K- بعدی از V است .
تنوع چو [ ویرایش ]
چو انواع چو (د، P 3 ) انواع جبری طرحی است که parametrizes درجه است د منحنی در P 3 . به شرح زیر ساخته شده است. بگذارید C در P 3 منحنی درجه d باشد ، سپس تمام خطوط موجود در P 3 را که منحنی C را در هم می کشد در نظر بگیرید. این یک درجه است د مقسوم علیه D C در G (2، 4)، Grassmannian از خطوط در P 3 . وقتی C متفاوت باشد ، با اتصال C به D متفاوت است ج ، فضای پارامترمنحنی هایدرجه d را به عنوان زیرمجموعه ای از فضایتقسیم کننده هایدرجه d Grassmannianبدست می آوریم: Chow (d، P 3 ).
طرح هیلبرت [ ویرایش ]
هیلبرت طرح Hilb ( X ) یک طرح مدول است. هر نقطه بسته Hilb ( X ) مربوط به یک زیر مجموعه بسته از یک طرح ثابت X است و هر زیر مجموعه بسته توسط چنین نقطه ای نشان داده می شود.
تعاریف [ ویرایش ]
چندین مفهوم مرتبط با چیزهایی وجود دارد که می توانیم آنها را فضاهای مدول بنامیم. هر یک از این تعاریف مفهوم متفاوتی از آنچه در نظر دارد برای مکانهای M برای نشان دادن اشیاء هندسی بطور رسمی ارائه می دهد.
فضاهای خوب مدول [ ویرایش ]
این مفهوم استاندارد است. کشاف، اگر ما یک فضای M که هر نقطه متر ε M مربوط به algebro هندسی شی U متر ، پس ما می توانیم این اشیاء به یک جمع آوری تکرار مکررات خانواده U بیش از M . (به عنوان مثال ، Grassmannian G ( k ، V ) دارای یک بسته مرتبه k است که فیبر آن در هر نقطه [ L ] ∊ G ( k ، V ) به سادگی زیر فضایی خطی L ⊂ V است .) Mفضای پایه ای از خانواده U نامیده می شود . ما می گوییم که چنین خانواده است جهانی اگر هر خانواده از اشیاء هندسی algebro T بیش از هر فضای پایه B است عقب نشینی از U به همراه یک نقشه منحصر به فرد B → M . فضای خوب مدول یک فضا است M است که پایه از یک خانواده جهانی است.
دقیقتر، فرض کنید که ما یک عمل کننده F از طرح به مجموعه، که اختصاص به یک طرح B مجموعه ای از تمام خانواده های مناسب از اشیاء با پایه B . فضای M یک فضای مدولار خوب برای F کتورکتور F است اگر M corepresents F ، یعنی یک ایزومورفیسم طبیعی τ وجود دارد: F → Hom (- ، M ) ، جایی که Hom (- ، M ) سرگرم کننده امتیازات است. این بدان معناست که M یک خانواده جهانی را در اختیار دارد. این خانواده ، خانواده ای در M است که مطابق با نقشه هویت 1 استم ∊ هوم ( م ، م ).
فضاهای مدول درشت [ ویرایش ]
فضاهای خوب مدول مطلوب است ، اما آنها همیشه وجود ندارند و ساخت آنها اغلب دشوار است ، بنابراین ریاضی دانان گاهی اوقات از مفهوم ضعیف تری استفاده می کنند ، ایده یک فضای مدول درشت. فضای M است فضای مدول درشت برای عمل کننده F اگر وجود داشته باشد τ تحول طبیعی وجود دارد: F → هوم (-، M ) و τ در میان چنین تحولات طبیعی جهانی است. مشخص تر، M یک فضای مدول درشت است F اگر هر خانواده T بیش از یک پایه B منجر به یک نقشه φ T : B → M و هر دو جسم Vو W (در نظر گرفته شده به عنوان یک خانواده بیش از یک نقطه) با همان نقطه M مطابقت دارند اگر و فقط اگر V و W ایزومورفیک هستند. بنابراین ، M فضایی است که برای هر شیئی که می تواند در یک خانواده ظاهر شود ، دارای یک امتیاز است و هندسه آن منعکس کننده راه های متفاوت بودن اشیاء در خانواده ها است. البته توجه داشته باشید که فضای درشت مدولار لزوماً هیچ خانواده ای از اشیاء مناسب را ندارد ، چه رسد به فضای جهانی.
به عبارت دیگر، یک فضای خوب مدول شامل هر دو یک فضای پایه M و خانواده جهانی U → M ، در حالی که یک فضای درشت مدول تنها فضای پایه M .
پشته های مدولی [ ویرایش ]
این اغلب اتفاق می افتد که اشیاء جالب هندسی با بسیاری از اتومبیل های طبیعی مجهز شده اند . این امر به طور خاص وجود یک فضای مدولار خوب را غیرممکن می کند (بطور مستقیم ، ایده این است که اگر L مقداری جسم هندسی باشد ، خانواده بی اهمیت L × [0،1] را می توان با شناسایی در یک خانواده پیچیده در دایره S 1 قرار داد. L × {0} با L × {1} از طریق یک های automorphism کوچک اما با اهمیت. حال اگر جریمه فضای مدول X وجود داشته است، نقشه S 1 → Xنباید ثابت باشد ، اما باید بر روی هر باز و بسته مناسب با بی اهمیت بودن ثابت باشد) ، هنوز هم گاهی اوقات می توانید فضای مدول های درشت بدست آورید. با این وجود ، این رویکرد ایده آل نیست ، زیرا وجود چنین فضاهایی تضمین نمی شود ، در صورت وجود آنها غالباً مفرد هستند و جزئیات مربوط به برخی خانواده های غیرواقعی اشیاء را که طبقه بندی می کنند ، از دست می دهند.
یک رویکرد پیچیده تر غنی سازی طبقه بندی با به یاد آوردن ایزومورفیسم است. به طور دقیق تر ، در هر پایه B می توان دسته خانواده های مربوط به B را مشاهده کرد که تنها ایزومورفیسم بین خانواده ها به عنوان مورفیزها در نظر گرفته شده است. سپس طبقه بندی فیبریدی در نظر گرفته می شود که به هر فضایی B ، گروه بندی خانواده های بالای B اختصاص می دهد . استفاده از این دسته ها که در گروهوئیدها برای توصیف یک مشکل مدولار وجود دارد ، به Grothendieck (196/60/60) برمی گردد. به طور کلی ، آنها نمی توانند توسط طرحها یا حتی فضاهای جبری نمایش داده شوند ، اما در بسیاری موارد ، ساختار طبیعی یک پشته جبری دارند .
پشته های جبری و استفاده از آنها برای تجزیه و تحلیل مشکلات ماژول ها در Deligne-Mumford (1969) به عنوان ابزاری برای اثبات غیر قابل تخریب فضای مدول (درشت) منحنی های یک جنس مشخص ظاهر شد. زبان پشته های جبری اساساً روشی منظم برای مشاهده ی دسته فیبر ایجاد می کند که مشکل ماژول ها را به عنوان "فضا" تشکیل می دهد ، و پشته ماژول بسیاری از مشکلات مدول بهتر رفتار می کند (مانند صاف) از فضای درشت ماژول های درشت.
مثالهای دیگر [ ویرایش ]
مدول منحنی ها [ ویرایش ]
اطلاعات بیشتر: ماژول های منحنی های جبری
پشته ماژول
هر دو پشته فوق دارای ابعاد 3 گرم -3 است. از این رو می توان با انتخاب مقادیر پارامترهای 3 g- 3 یک منحنی گره پایدار را کاملاً مشخص کرد ، هنگامی که g > 1. در جنس پایین ، باید با کم کردن تعداد آنها ، حضور خانواده های صاف از اتومبیل را نشان داد. کره ریمان دقیقاً یک منحنی پیچیده از جنس صفر وجود دارد ، و گروه ایزومورفیسم آن PGL است (2). از این رو ، بعد
کم رنگ (فضای منحنی های صفر جنس) - کم رنگ (گروه اتومبیل) = 0 - کم (PGL (2)) = −3.
به همین ترتیب ، در جنس 1 ، یک فضای منحنی یک بعدی وجود دارد ، اما هر منحنی چنین دارای یک گروه یک بعدی از اتومبیل ها است. از این رو ، پشته
همچنین می توان با در نظر گرفتن پشته ماژول های جنس g منحنی گره با n نقاط مشخص شده ، مشکل را غنی سازی کرد . گفته می شود چنین منحنی های مشخص اگر زیر مجموعه ای از اتمورفیسم های منحنی که نقاط مشخص شده را ثابت می کنند ، پایدار هستند ، محدود است. در نتیجه پشته مدول صاف (و یا ثابت) جنس گرم منحنی با N نقاط عالمت نشان داده می
مورد مورد علاقه خاص پشته ماژول ها است
مدول انواع [ ویرایش ]
در ابعاد بالاتر ، ساخت و مطالعه واحدهای مختلف جبر دشوارتر است. به عنوان مثال ، آنالوگ بعدی بالاتر فضای ماژولهای منحنی بیضوی که در بالا مورد بحث قرار گرفت فضای مدولار انواع آبلیان ، مانند انواع ماژولار سیگل است . این مشکل اساسی در نظریه فرم مدولار سیگل است. همچنین به انواع Shimura مراجعه کنید .
ماژول های بسته های وکتور [ ویرایش ]
یکی دیگر از مشکلات مهم ماژول ها ، درک هندسه (زیر پست های مختلف) مدول پشته Vect n ( X ) بسته های بردار درجه n بر روی انواع جبری ثابت X است . این پشته بیشتر مورد مطالعه قرار گرفته است که X یک بعدی است و به خصوص وقتی که n برابر با یک باشد. در این حالت ، فضای درشت مدولار طرح Picard است که مانند فضای ماژول های منحنی ها ، قبل از اختراع پشته ها مورد مطالعه قرار گرفت. هنگامی که بسته های دارای درجه 1 و درجه صفر هستند ، مطالعه فضای مدول های درشت مطالعه انواع ژاکوبین است .
در برنامه های کاربردی برای فیزیک ، تعداد واحدهای بسته های بردار و مشکل نزدیک مربوط به تعداد مدول های بسته های اصلی G در تئوری سنج قابل توجه است . [ نیاز به استناد ]
حجم فضای ماژول ها [ ویرایش ]
ژئودزیک ساده و حجم Weil-Peterson از فضای مدولار از سطوح مرزی با ریمان.
روشهای ساخت فضاهای مدولار [ ویرایش ]
فرمول مدرن از مشکلات ماژول ها و تعریف فضاهای ماژول از نظر جداول ماژول ها (یا به طور کلی دسته بندی های فیبروئیدی در گروپوئیدها ) و فضاهایی (تقریبا) که نمایانگر آنهاست ، مربوط به گروتهندیک (1960/61/60) است که در آن توضیح داده است. چارچوب کلی ، رویکردها و مشکلات اصلی با استفاده از فضاهای Teichmüller در هندسه تحلیلی پیچیده به عنوان نمونه. این گفتگوها ، به طور خاص ، روش سخت ساخت فضاهای مدولار را ابتدا با تشدید مشکل ماژول های مورد بررسی توصیف می کند.
به طور دقیق تر ، وجود اتوفرمیسم های غیرواقعی در اشیاء طبقه بندی شده ، امکان فضای مناسب مدولار را غیرممکن می کند. با این حال ، اغلب می توان یک مسئله تعدیل شده مدول را در طبقه بندی اشیاء اصلی به همراه داده های اضافی در نظر گرفت ، به گونه ای انتخاب شده که هویت تنها اتومبیل سازی است که به داده های اضافی نیز احترام می گذارد. با انتخاب مناسب از داده های سفت و سخت ، مشکل مدول اصلاح شده یک فضای مدولار (ریز) T خواهد داشت که غالباً به عنوان زیر مجموعه یک طرح مناسب یا طرح مناسب Quot توصیف می شود . علاوه بر این ، داده های سفت و سخت به گونه ای انتخاب می شوند که به یک بسته اصلی با گروه ساختار جبری G مطابقت داشته باشند.. بنابراین می توان با استفاده از عملکرد G از مشکل سخت به حالت اولیه برگرداند و مشکل ساخت فضای ماژول ها به مسئله یافتن یک طرح (یا فضای عمومی تر) تبدیل می شود که (به معنای مناسب قوی) خارج قسمت T / G از T توسط عمل G . به طور کلی ، آخرین مشکل راه حل را نمی پذیرد. با این حال ، این تئوری با استفاده از تئوری ثابت هندسی پیشگامانه (GIT) ، توسعه یافته توسط دیوید مامفورد در سال 1965 مورد بررسی قرار گرفته است ، که نشان می دهد در شرایط مناسب ، حقیقت واقعاً وجود دارد.
برای دیدن اینکه چگونه این ممکن است کار کند ، مشکل پارامتر کردن منحنی های صاف از جنس g > 2. را در نظر بگیرید. یک منحنی صاف بهمراه یک سیستم خطی کامل از درجه d > 2 g معادل زیر مجموعه یک بعدی بسته از فضای پروژکتور P d است. -g . در نتیجه ، فضای ماژول های منحنی های صاف و سیستم های خطی (برآورده شدن معیارهای خاص) ممکن است در طرح هیلبرت از یک فضای پروژکتور به اندازه کافی بالا تعبیه شود. این مکان H در طرح هیلبرت عملی از PGL ( n ) دارد که عناصر سیستم خطی را با هم مخلوط می کند. در نتیجه ، فضای مدولهای منحنیهای صاف سپس به عنوان قطر H بازیابی می شود توسط گروه خطی عمومی پیش بینی شده.
یک رویکرد کلی دیگر در درجه اول با مایکل آرتین همراه است . در اینجا ایده این است که با هدف از نوع شروع شود تا طبقه بندی شود و نظریه تغییر شکل آن را مطالعه کند . این بدان معنی است که ابتدا تغییر شکلهای نامتناهی ایجاد می شود ، سپس برای قضیه های پیش نمایش بودن جذاب می شود تا اینها را در یک جسم بیش از یک پایه رسمی قرار دهند. در مرحله بعد ، درخواست تجدید نظر در مورد قضیه وجود رسمی گروتندیك شیء مورد نظر را از طریق پایه ای كه یك حلقه محلی كامل است فراهم می كند. این جسم را می توان از طریق قضیه تقریبی آرتین با یک جسم تعریف شده بر روی یک حلقه تولید شده به طور تقریبی تقریب داد . طیفاین حلقه دوم را می توان بعنوان نوعی نمودار مختصات در فضای مدول مورد نظر مشاهده کرد. با چسباندن به اندازه کافی از این نمودارها ، می توانیم این فضا را بپوشانیم ، اما نقشه از اتحاد طیف های ما به فضای مدول ها ، به طور کلی ، تعداد زیادی از یک خواهد بود. بنابراین ، ما رابطه هم ارزی با سابق را تعریف می کنیم . در واقع ، اگر اشیاء روی هر یک از هم همرفت باشند ، دو نقطه معادل است. این یک طرح و یک رابطه هم ارزی را می دهد ، که برای تعریف یک فضای جبری (در واقع یک پشته جبری اگر مراقب باشیم) کافی است اگر همیشه یک طرح نباشد.
در فیزیک [ ویرایش ]
اطلاعات بیشتر: مدول (فیزیک)
اصطلاح فضای ماژول ها در فیزیک گاهی اوقات مورد استفاده قرار می گیرد تا به طور خاص به فضای مدولار از مقادیر انتظار خلاء مجموعه ای از زمینه های مقیاس یا به فضای مدولهای پس زمینه های رشته ای ممکن اشاره شود .
فضاهای ماژول نیز در فیزیک در نظریه میدان کوهیولوژی ظاهر می شوند ، جایی که می توان از انتگرال های مسیر فاینمن برای محاسبه تعداد تقاطع فضاهای مختلف مدول جبری استفاده کرد.
منبع
https://en.wikipedia.org/wiki/Moduli_space#Coarse_Moduli_Spaces
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.