1-فضای هیلبرت

توسط علی رضا نقش نیلچی | دوشنبه شانزدهم تیر ۱۳۹۹ | 19:16

در ریاضیات ، فضاهای هیلبرت (به نام دیوید هیلبرت ) اجازه می دهد تا روش های جبر خطی و حساب دیفرانسیل و انتگرال را از فضاهای برداری اقلیدسی (بعد محدود) به فضاهایی که ممکن است بینهایت بعدی باشند تعمیم دهند . فضاهای هیلبرت به طور طبیعی و اغلب در ریاضیات و فیزیک به وجود می آیند ، معمولاً به عنوان فضاهای تابعی . به طور رسمی، فضای هیلبرت یک فضای برداری مجهز به یک ضرب داخلی است که تابع فاصله ای را القا می کند که برای آن فضا یک فضای متریک کامل است . فضای هیلبرت یک مورد خاص از فضای باناخ است .

فضاهای هیلبرت در دهه اول قرن بیستم توسط دیوید هیلبرت ، ارهارد اشمیت و فریگیس ریس مورد مطالعه قرار گرفت . آنها ابزارهای ضروری در تئوری های معادلات دیفرانسیل جزئی ، مکانیک کوانتومی ، تحلیل فوریه (که شامل کاربردهایی برای پردازش سیگنال و انتقال حرارت است )، و نظریه ارگودیک (که زیربنای ریاضی ترمودینامیک را تشکیل می دهد ) هستند. جان فون نویمان اصطلاح فضای هیلبرت را برای مفهوم انتزاعی که زیربنای بسیاری از این کاربردهای متنوع است ابداع کرد. موفقیت روش‌های فضایی هیلبرت، دوران بسیار پرباری را برای تحلیل عملکردی آغاز کرد . جدای از فضاهای برداری کلاسیک اقلیدسی، نمونه هایی از فضاهای هیلبرت شامل فضاهای توابع انتگرال پذیر مربع ، فضاهای دنباله ای ، فضاهای سوبولف متشکل از توابع تعمیم یافته و فضاهای هاردی توابع هولومورفیک هستند .

شهود هندسی نقش مهمی در بسیاری از جنبه های نظریه فضایی هیلبرت ایفا می کند. مشابهات دقیق قضیه فیثاغورث و قانون متوازی الاضلاع در فضای هیلبرت وجود دارد. در یک سطح عمیق تر، طرح ریزی عمود بر روی یک زیرفضای خطی نقش مهمی در مسائل بهینه سازی و سایر جنبه های تئوری ایفا می کند. یک عنصر از فضای هیلبرت را می توان به طور منحصر به فرد با مختصات آن با توجه به یک پایه متعارف ، در قیاس با مختصات دکارتی در هندسه کلاسیک، مشخص کرد. هنگامی که این مبنا به طور قابل شمارش نامتناهی باشد ، امکان شناسایی فضای هیلبرت را با فضای دنباله های نامتناهی که قابل جمع مربع هستند را می دهد . فضای اخیر اغلب در ادبیات قدیمی تر به عنوان فضای هیلبرت شناخته می شود .

تعریف و تصویر

[ ویرایش ]

مثال انگیزشی: فضای برداری اقلیدسی

[ ویرایش ]

یکی از آشناترین نمونه‌های فضای هیلبرت، فضای برداری اقلیدسی است که از بردارهای سه‌بعدی تشکیل شده است که با R3 نشان داده می‌شوند و مجهز به ضرب نقطه‌ای هستند . حاصل ضرب نقطه ای دو بردار x و y را می گیرد و یک عدد حقیقی x ⋅ y تولید می کند . اگر x و y در مختصات دکارتی نشان داده شوند ، حاصل ضرب نقطه ای با تعریف می شود. ${\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\end{pmatrix}}\cdot {\begin{pmatrix}y_{1}\\y_{2}\\y_{3}\end{pmatrix}}=x_{1}y_{1}+x_{2}y_{2}+x_{3 }y_{3}\,.$

ضرب نقطه ای ویژگی ها را برآورده می کند [ 1 ]

در x و y متقارن است : x ⋅ y = y ⋅ x .
در متغیر اولش خطی است : ( a x 1 + b x 2 ) ⋅ y = a ( x 1 ⋅ y ) + b ( x 2 ⋅ y ) برای هر اسکالر a , b و بردارهای x 1 , x 2 , و y
مثبت قطعی است : برای همه بردارهای x , x ⋅ x ≥ 0 , با برابری اگر و فقط اگر x = 0 باشد .

عملیات روی جفت بردارها که مانند حاصل ضرب نقطه‌ای، این سه ویژگی را برآورده می‌کند، به عنوان حاصلضرب داخلی (حقیقی) شناخته می‌شود . فضای برداری مجهز به چنین ضرب داخلی به عنوان فضای ضرب داخلی (حقیقی) شناخته می شود . هر فضای ضرب داخلی با ابعاد محدود، فضای هیلبرت است. [ 2 ] ویژگی اصلی حاصلضرب نقطه‌ای که آن را به هندسه اقلیدسی متصل می‌کند این است که هم به طول (یا هنجار ) یک بردار که با ‖ x نشان داده می‌شود و هم به زاویه θ بین دو بردار x و y مرتبط است . ابزار فرمول. 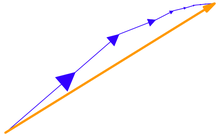$\mathbf {x} \cdot \mathbf {y} =\left\|\mathbf {x} \right\|\left\|\mathbf {y} \right\|\,\cos \theta \, .$

کامل بودن به این معنی است که یک سری از بردارها (به رنگ آبی) منجر به یک بردار جابجایی خالص کاملاً تعریف شده (به رنگ نارنجی) می شود.

محاسبات چند متغیره در فضای اقلیدسی بر توانایی محاسبه محدودیت ها و داشتن معیارهای مفید برای نتیجه گیری از وجود محدودیت ها متکی است. یه سری ریاضی $\sum _{n=0}^{\infty }\mathbf {x} _{n}$ متشکل از بردارها در R3 کاملاً همگرا است به شرطی که مجموع طولها به صورت یک سری معمولی از اعداد حقیقی همگرا شوند: [ 3 ]. $\sum _{k=0}^{\infty }\|\mathbf {x} _{k}\|<\infty \,.$

درست مانند یک سری از اسکالرها، یک سری از بردارها که مطلقاً همگرا می شوند نیز به بردار حدی L در فضای اقلیدسی همگرا می شوند، به این معنا که"کبه عنوان ن. ${\Biggl \|}\mathbf {L} -\sum _{k=0}^{N}\mathbf {x} _{k}{\Biggr \|}\to 0\quad {\text {به عنوان }}N\to \infty \,.$

این ویژگی کامل بودن فضای اقلیدسی را بیان می کند: این که مجموعه ای که مطلقاً همگرا می شود به معنای معمولی نیز همگرا می شود.

فضاهای هیلبرت اغلب بر روی اعداد مختلط گرفته می شود . صفحه مختلط که با C نشان داده شده است مجهز به مفهوم قدر است، مدول مختلط | z | که به عنوان جذر حاصلضرب z با مزدوج مختلط آن تعریف می شود :. $|z|^{2}=z{\overline {z}}\,.$

اگر z = x + iy تجزیه z به قسمت های حقیقی و خیالی آن باشد، مدول آن طول دو بعدی معمول اقلیدسی است:. $|z|={\sqrt {x^{2}+y^{2}}}\,.$

حاصل ضرب درونی یک جفت اعداد مختلط z و w حاصل ضرب z با مزدوج مختلط w است : $\langle z,w\rangle =z{\overline {w}}\,.$

این دارای ارزش مختلط است. بخش حقیقی 〈 z ، w 〉 حاصل ضرب نقطه اقلیدسی دو بعدی معمول را به دست می‌دهد .

مثال دوم فضای C 2 است که عناصر آن جفت اعداد مختلط z = ( z 1 , z 2 ) هستند . سپس حاصل ضرب درونی z با بردار دیگری w = ( w 1 , w 2 ) با〈. $\langle z,w\rangle =z_{1}{\overline {w_{1}}}+z_{2}{\overline {w_{2}}}\,.$

سپس بخش حقیقی 〈 z ، w 〉 حاصل ضرب نقطه اقلیدسی چهار بعدی است. این ضرب داخلی متقارن هرمیتی است ، به این معنی که نتیجه تبادل z و w مزدوج مختلط است:. $\langle w,z\rangle ={\overline {\langle z,w\rangle }}\,.$

تعریف

[ ویرایش ]

فضای هیلبرت یک فضای ضرب داخلی حقیقی یا مختلط است که همچنین یک فضای متریک کامل با توجه به تابع فاصله القا شده توسط ضرب داخلی است. [ 4 ]

اینکه بگوییم یک فضای برداری مختلط H یک فضای ضرب درونی مختلط است به این معنی است که یک ضرب درونی وجود دارد $\langle x,y\rangle$ ارتباط دادن یک عدد مختلط به هر جفت عنصر $x,y$ از H که ویژگی های زیر را برآورده می کند:

ضرب داخلی متقارن مزدوج است. یعنی حاصلضرب داخلی یک جفت عنصر برابر است با مزدوج مختلط حاصلضرب داخلی عناصر مبادله شده: $\langle y,x\rangle ={\overline {\langle x,y\rangle }}\,.$ نکته مهم این است که $\langle x,x\rangle$ یک عدد حقیقی است
حاصلضرب داخلی در اولین متغیر [ nb 1 ] خود خطی است . برای همه اعداد مختلط $a$ و، $b,$ . $\langle ax_{1}+bx_{2},y\rangle =a\langle x_{1},y\rangle +b\langle x_{2},y\rangle \,.$
${\begin{alignedat}{4}\langle x,x\rangle >0&\quad {\text{ if }}x\neq 0,\\\langle x,x\rangle =0&\quad {\ متن{ if }}x=0\,.\end{alignedat}}$

از خواص 1 و 2 چنین بر می آید که یک ضرب داخلی مختلط ضد خطی است که در متغیر دوم خود به آن خطی مزدوج نیز گفته می شود ، به این معنی که. $\langle x,ay_{1}+by_{2}\rangle ={\bar {a}}\langle x,y_{1}\rangle +{\bar {b}}\langle x,y_{ 2}\rangle \,.$

فضای ضرب داخلی حقیقی نیز به همین صورت تعریف می شود، با این تفاوت که H یک فضای برداری حقیقی است و حاصلضرب داخلی مقادیر حقیقی را می گیرد. چنین ضرب داخلی یک نقشه دوخطی خواهد بود و $(H,H,\langle \cdot,\cdot \rangle )$ یک سیستم دوگانه تشکیل خواهد داد . [ 5 ]

هنجار تابع با ارزش حقیقی است، $\|x\|={\sqrt {\langle x,x\rangle }}\,,$ و فاصلهد $d$ بین دو نقطه $x,y$ در H بر حسب هنجار توسط تعریف شده استد. $d(x,y)=\|xy\|={\sqrt {\langle xy,xy\rangle }}\,.$

اینکه این تابع یک تابع فاصله است، اولاً به این معنی است که متقارن است $x$ و، $y,$ دوم اینکه فاصله بینx $x$ و خودش صفر است و در غیر این صورت فاصله بین $x$ و $y$ باید مثبت باشد و در نهایت نابرابری مثلث برقرار است، به این معنی که طول یک پایه مثلث xyz نمی تواند از مجموع طول های دو پایه دیگر تجاوز کند:د $d(x,z)\leq d(x,y)+d(y,z)\,.$

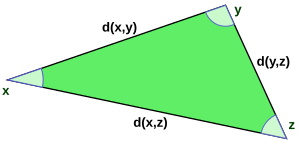
این ویژگی آخر در نهایت نتیجه نابرابری اساسی تر کوشی-شوارتز است که ادعا می کند $\left|\langle x,y\rangle \right|\leq \|x\|\|y\|$ با برابری اگر و فقط اگر $x$ و $y$ به صورت خطی وابسته هستند .

با یک تابع فاصله که به این شکل تعریف شده است، هر فضای ضرب داخلی یک فضای متریک است و گاهی اوقات به عنوان فضای پیش از هیلبرت شناخته می شود . [ 6 ] هر فضای پیش از هیلبرت که علاوه بر آن یک فضای کامل نیز باشد ، فضای هیلبرت است. [ 7 ]

کامل بودن H با استفاده از شکلی از معیار کوشی برای دنباله‌های H بیان می‌شود : فضای H پیش از هیلبرت کامل است اگر هر دنباله کوشی با توجه به این هنجار به عنصری در فضا همگرا شود. کامل بودن را می توان با شرط معادل زیر مشخص کرد: اگر یک سری از بردارها $\sum _{k=0}^{\infty }u_{k}$ کاملاً به این معنا همگرا می شود که، $\sum _{k=0}^{\infty }\|u_{k}\|<\infty \,,$ سپس سری در H همگرا می شود ، به این معنا که مجموع جزئی به عنصری از H همگرا می شوند . [ 8 ]

فضاهای هیلبرت به عنوان یک فضای هنجاری کامل، طبق تعریف، فضاهای باناخ نیز هستند . به این ترتیب آنها فضاهای برداری توپولوژیکی هستند که در آنها مفاهیم توپولوژیکی مانند باز بودن و بسته بودن زیر مجموعه ها به خوبی تعریف شده است . مفهوم زیرفضای خطی بسته یک فضای هیلبرت از اهمیت ویژه ای برخوردار است که با حاصلضرب درونی ناشی از محدودیت نیز کامل است (مجموعه ای بسته در یک فضای متریک کامل) و بنابراین به خودی خود یک فضای هیلبرت است.

مثال دوم: فاصله های دنباله

[ ویرایش ]

فضای دنباله l 2 شامل تمام دنباله های نامتناهی z = ( z 1 , z 2 , ... ) از اعداد مختلط است به طوری که سری زیر همگرا می شوند : [ 9 ] $\sum _{n=1}^{\infty }|z_{n}|^{2}$

حاصلضرب داخلی در l 2 به صورت زیر تعریف می شود:، $\langle \mathbf {z} ,\mathbf {w} \rangle =\sum _{n=1}^{\infty }z_{n}{\overline {w_{n}}}\,,$

این سری دوم در نتیجه نابرابری کوشی-شوارتز و همگرایی سری قبلی همگرا می شود.

کامل بودن فضا پابرجاست به شرطی که هر گاه یک سری از عناصر از l 2 به طور مطلق (در هنجار) همگرا شوند، سپس به عنصر l 2 همگرا شود . این اثبات در تجزیه و تحلیل ریاضی پایه است ، و اجازه می‌دهد تا سری‌های ریاضی از عناصر فضا به آسانی سری‌های اعداد مختلط (یا بردارها در فضای اقلیدسی با ابعاد محدود) دستکاری شوند. [ 10 ]

مشخصات وب

در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
09132003030

ریاضیات

آموزش ریاضی