روش Runge-Kutta
در [2] مشخص شده است که در میان مدل های استفاده از معادلات دیفرانسیل، معادلات دیفرانسیل معمولی (ODE) اغلب برای توصیف مشکلات مختلف فیزیکی، به عنوان مثال، حرکت سیارات در میدان گرانشی مانند مشکل کپلر، آونگ ساده ، مدارهای الکتریکی و مشکلات سینتیکی شیمیایی. ODE دارای فرم است:
|
y ¢ (x) = f (x، y (x)) |
(1) |
جایی که x متغیر مستقل است که اغلب به زمان در یک مشکل فیزیکی اشاره دارد و متغیر وابسته y (x)، راه حل است. از آنجا که y (x) می تواند یک تابع ارزش بردار بعدی N باشد، دامنه و محدوده معادله دیفرانسیل معمول، f و راه حل y توسط:
|
(2) |
ODE بالا نامیده می شود غیر خودمختار است، زیرا f یک تابع از x و y است. با این حال، به سادگی با معرفی یک متغیر اضافی، که همیشه دقیقا با x برابر است، می تواند به راحتی در یک فرم معادل «مستقل» بازنویسی شود:
y ¢ (x) = f (y (x))
جایی که f تنها تابع y است.
متأسفانه، بسیاری از مشکلات مربوط به ODE دقیقا نمیتوان حل کرد. به همین دلیل توانایی عددی تقریب این روش ها بسیار مهم است [2].
راه حل عددی از ODE ها مهم ترین تکنیک است که تا به حال در پویایی زمان مداوم توسعه یافته است. از آنجا که اکثر ODE ها از نظر تحلیلی قابل حل نیستند، ادغام عددی تنها راه کسب اطلاعات در مورد مسیر است. بسیاری از روش های مختلف پیشنهاد شده و مورد استفاده در تلاش برای حل دقیق، انواع مختلف ODE است. با این حال، تعداد زیادی از روش های شناخته شده و استفاده شده در جهان (یعنی Runge-Kutta، Adam-Bashforth-Moulton و فرمول تفاوت عقب مانده) وجود دارد. همه اینها سیستم دیفرانسیل را برای ایجاد یک معادله یا نقشه اختلاف [3] را کاهش می دهند.
این روش ها، نقشه های مختلفی را از همان معادله به دست می آورند، اما آنها هدف مشابهی دارند. که دینامیک نقشه ها باید به طور دقیق مطابق با پویایی معادلات دیفرانسیل باشد. از خانواده الگوریتم Runge-Kutta، روش های شناخته شده و مورد استفاده برای ادغام عددی [4] آمده است.
با ظهور رایانه ها، روش های عددی در حال حاضر به طور فزاینده ای جذاب و کارآمد برای به دست آوردن راه حل های تقریبی برای معادلات دیفرانسیل است که تا کنون ثابت شده است و حتی تحلیلی غیرممکن است. با این حال، برای این کار، ما به ویژه در کلاس روش های اولیه پیشنهاد شده توسط دیوید رنج (1856-1927) [5]، یک ریاضیدان و فیزیکدان آلمانی، علاقه مند شدیم و توسط یکی دیگر از ریاضیدان آلمانی به نام ویلهلم Kutta (1944-1867) [6] به سیستم معادلات؛ یک روش معمول به روش Runge-Kutta اشاره دارد.
مواد و روش
دینامیک روش Runge-Kutta
ما IVP را در نظر می گیریم:
|
y ¢ = f (x، y)، y (a) = α |
(3) |
روش Runge-Kutta برای حل معادله (3)، روشهای یک مرحله ای هستند که برای تقریب متدهای سری تیلور طراحی شده اند، اما مزیت این است که نیازی به ارزیابی صریح مشتقات f (x، y) ندارند ، که x اغلب زمان را نشان می دهد (t). ایده اصلی این است که از ترکیب خطی از مقادیر f (x، y) برای تقریبی y (x) استفاده کنیم. این ترکیب خطی تا حد ممکن نزدیک تر می شود، با مجموعه ی تیلور برای y (x) برای به دست آوردن روش های بالاترین احتمال ممکن است. فرض می شود که مقدار اولیه (x 0، y 0 ) با توجه به معادله انحصاری نیست و یک راه حل وجود دارد که می تواند در مجموعه تیلور توسعه یابد . [7]
بر طبق [8]، [9]، روش Runge-Kutta S-stage، به صورت زیر تعریف می شود:
|
(4) |
|
|
(5) |
|
|
(6) |
با استفاده از
k = [k 1 ، k 2 ، ...، k s ]
دامنه ها،
b = [b 1 ، b 2 ، ...، b s ]
وزن ها و
c = [c 1 ، c 2 ، ...، c s ]
ابسوسا
روش SK مرحله RK نیاز به ارزیابی عملکرد توابع در هر مرحله دارد. هر یک از توابع k r = (x، y، h)، r = 1، 2 ... s ممکن است به عنوان تقریبی به مشتق y ¢ (x) تفسیر شود و تابع f (x، y، h) به عنوان وزن میانگین این تقریبها. ثبات، مستلزم آن است که Σ s r = 1 b r = 1 باشد.
تشخیص یک روش Runge-Kutta S-Stage
با توجه به [1]، سه روش برای استخراج روش Runge-Kutta وجود دارد:
- · گسترش سری تیلور؛
- · مفهوم جبری درختان ریشه ای
- · جبر کامپیوتر
در این مقاله، بحث ما بر روی روش گسترش سری تیلور خواهد بود.
فرایند تولید یک روش داده شده توسط RK توسط گسترش سری تیلور می تواند به سه مرحله زیر خلاصه شود:
- · مرحله 1 :
به دست آوردن مجموعه سری تیلور k r (دامنه ها) تعریف شده توسط:
|
k r = f (z r ، y n + hΣ s a rj k j ) |
(7) |
جایی که: z r = x n + c r h، r = 1 (1) s در مورد نقطه (x n ، y n ) در فضای راه حل.
- · مرحله 2:
قرار دادن این گسترش ها و c r (c r = Σ s j = 1 a rj ، r = 1 (1) به بیان روش RK عمومی S-مرحله، به صورت زیر است:
|
f RK = Σ s b j k j ، s≥1 |
(8) |
- · مرحله 3:
مقایسه ضرایب در قدرت ساعت برای هر دو تابع افزایش F RK از روش رانگ کوتا مرتبه چهار-داده شده در معادله (8) بالا و عملکرد افزایش F T برای تیلور روش بسط توسط مشخص شده
[8]، [9] و [10] نشان داده شده است که اگر این توابع با شرایط در h p موافق باشند ، این فرایند به ترتیب p است. مجموع ضرایب ناشناخته { bj ، c r ، a rj ، j = 1 (1s)} به طور معمول بیش از تعداد معادلات است و پارامترهای آزاد را به ما می دهد که می توانیم مقادیر آن را تعیین کنیم [11].
ریچاردسون استخراج
یک نقص عمده در روش Runge-Kutta این است که برای مشاهده خطاها دشوار و پیچیده است. با توجه به [8]، " محدوده خطاهای مختلط محلی، پایه مناسب برای نظارت بر خطای کوتاه شدن محلی را ایجاد نمی کند، با توجه به ساخت یک سیاست کنترل مرحله ای مشابه آنچه که برای روش پیش بینی کننده اصلاح شده طراحی شده است. آنچه که مورد نیاز است، در عوض یک محدوده، تخمین قابل قبول محاسبه خطای تخریب محلی است، شبیه به آنچه که توسط دستگاه Milne برای جفت های پیش بینی کننده-اصلاح کننده به دست آمده است . "
برآوردی که ما ارائه می دهیم ناشی از کاربرد فرآیند رویکرد تعلیق به حد است، که در غیاب به عنوان Extrapolation ریچاردسون شناخته می شود. این شامل حل مسئله دو بار با استفاده از اندازه گام ها h و 2h است.
در زیر فرض محلی سازی که هیچ خطای قبلی ایجاد نشده است، می توانیم نوشت:
|
y (x n + 1 ) - y n + 1 = T n + 1 = φ (x n ، y (x n )) h p + 1 + o (h p + 2 ) |
(10) |
جایی که p به ترتیب روش Runge-Kutta است، φ (x n ، y (x n )) h p + 1 خطای اصلی تکه تکه شدن محلی است.
بعد، ما y * n + 1 ، تقریبی دوم به y (x n + 1 ) محاسبه می کنیم ، که با استفاده از همان روش در x n-1 با steplenght 2h بدست می آید. بر اساس یک فرض محلی سازی، از این می شود که:
|
y (x n + 1 ) - y * n + 1 = φ (x n-1 ، y (x n-1 )) (2h) p + 1 + o (h p + 2 ) |
(11) |
و در گسترش φ (x n-1 ، y (x n-1 )) در مورد (x n ، y n ):
|
y (x n + 1 ) - y * n + 1 = φ (x n ، y (x n )) (2h) p + 1 + o (h p + 2 ) |
(12) |
در تفریق (10) از (12)، ما دریافت می کنیم:
y (x n + 1 ) - y * n + 1 = (2 p + 1 - 1) φ (x n ، y (x n )) h p + 1 + o (h p + 2 )
بنابراين، خطاي اصلي ترك كردن موضعي كه به عنوان برآورد خطاي كوتاه مدت در نظر گرفته مي شود، مي تواند به صورت زير باشد:
|
φ (x n ، y (x n )) h p + 1 = Tn + 1 = (y (x n + 1 ) - y * n + 1 ) / (2 p + 1 - 1) |
(13) |
=>
|
T n + 1 = (y (x n + 1 ) -y * n + 1 ) / (2 p + 1 -1) |
(14) |
معادله (14) به معنای به دست آوردن تخمین های سریع خطاهای مختلط محلی در محاسبات با استفاده از هر Runge-Kutta S است، بدون اینکه اولین راه حل دقیق را بدست آوریم.
آزمایشات عددی
ما به وسیله حل معادله (14) با حل مسئله ارزش اولیه خودمختار، اثربخشی روش Extrapolation ریچاردسون را نشان خواهیم داد.
y '= x + y؛ y (0) = 1 (جواب دقیق: y E = 2e x -x-1 )
در steplenghts h = 0.1 و h = 0.2 است.
روش ما برای تحقیق ما از روش Runge-Kutta شش مرحله بسیار کارا با پنج قاشق غذاخوری استفاده می کند:
از این پس ما به این روش به عنوان RK65 اشاره خواهیم کرد.
نتایج و بحث ها
نتایج زیر ارائه شده است:
جدول .1 نتایج آزمایش تجربی
|
ساعت |
ایکس |
RK65 |
دقیق |
خطا واقعی |
|
|
0.0 |
1.0 |
1.0 |
0.0 |
|
0.1 |
0.1 |
1.110341796 |
1.110341836 |
4.01513E-08 |
|
|
0.2 |
1.242805427 |
1.242805516 |
8.93203E-08 |
|
|
0.3 |
1.399717467 |
1.399717615 |
1.48152E-07 |
|
|
0.4 |
1.583649177 |
1.583649395 |
2.18283E-07 |
|
|
0.5 |
1.79744224 |
1.797442541 |
3.014E-07 |
|
|
0.6 |
2.044237201 |
2.044237601 |
3.99781E-07 |
|
|
0.7 |
2.327504899 |
2.327505415 |
5.15941E-07 |
|
|
0.8 |
2.651081205 |
2.651081857 |
6.51985E-07 |
|
|
0.9 |
3.019205412 |
3.019206222 |
8.10314E-07 |
|
|
1.0 |
3.436562662 |
3.436563657 |
9.94918E-07 |
|
|
0.0 |
1.000000000 |
1.000000000 |
0،00000000000 |
|
0.2 |
0.2 |
1.242803057 |
1.242805516 |
2.45932E-06 |
|
|
0.4 |
1.583643388 |
1.583649395 |
6.00728E-06 |
|
|
0.6 |
2.044226595 |
2.044237601 |
1.10058E-05 |
|
|
0.8 |
2.651063934 |
2.651081857 |
1.7923E-05 |
|
|
1.0 |
3.436536293 |
3.436563657 |
2.73639E-05 |
معمولا برای بدست آوردن خطاها، راه حل دقیق و تقریب های عددی به دست می آید و تفاوت آنها در هر مرحله خطا در هر مرحله می دهد. هدف ما در این مقاله نشان دادن این است که در واقع ممکن است چنین اشتباهی را بدون نیاز به راه حل دقیق برای اولین بار بدست آوریم.
بعد، معادله (14) برای برآورد خطا استفاده می شود که به راه حل های دقیق بستگی ندارد.
به یاد آوردن معادله (14):
T n + 1 = (y (x n + 1 ) -y * n + 1 ) / (2 p + 1 -1)
جایی که: y n + 1 محلول تقریبی با h = 0.1 است؛ y * n + 1 راه حل تقریبی با h = 0.2 است؛ p روش روش است یعنی p = 5.
از این رو معادله (14) می شود:
T n + 1 = (y (x n + 1 ) -y * n + 1 ) / 63
باید اشاره کرد که آنچه معادله (14) ارائه می دهد، برآورده می شود، اما این برآوردها به ما می گوید که طبیعت و نظم اشتباهاتی که ما با آن مواجه هستیم و زمانی که راه حل های تحلیلی قابل دستیابی نیست، این روش تنها گزینه ای است که در دسترس است .
در x = 0.2: T n + 1 = 1.242805427 - 1.242803057 / 63 = 3.7619E-08
در x = 0.4: T n + 1 = 1.583649177 - 1.583643388 / 63 = 9.189E - 08
در x = 0.6: T n + 1 = 2.044237201 - 2.044226595 / 63 = 1.684E - 07
در x = 0.8: T n + 1 = 2.651081205 - 2.651063934 / 63 = 2.74E - 07
در x = 1.0: T n + 1 = 3.43656362 - 3.436536293 / 63 = 4.186E - 07
مقایسه مقادیر خطا و خطای واقعی در جدول 2 نشان داده شده است.
جدول 2 خلاصه ای از نتایج برای اشتباهات واقعی و خطاهای تخمینی
|
ایکس |
خطا واقعی |
برآورد خطا |
|
0.2 |
8.90E-08 |
3.76E-08 |
|
0.4 |
2.18E-07 |
9.19E-08 |
|
0.6 |
4.00E-07 |
1.68E-07 |
|
0.8 |
6.52E-07 |
2.74E-07 |
|
1.0 |
9.95E-07 |
4.19E-07 |
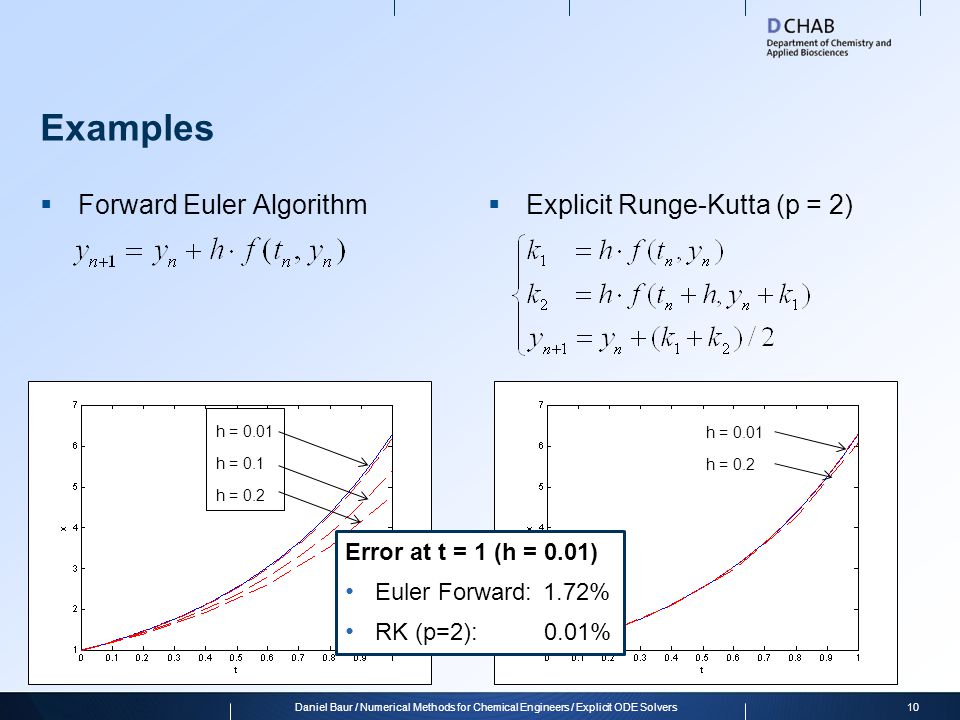
شکل 1 نمودار مقایسه خطاهای واقعی و خطاهای تخمینی
از شکل 1 ما می توانیم از منحنی های راه حل ببینیم که منحنی برآورد خطا با استفاده از استخراج ریچاردسون بسیار نزدیک به منحنی راه حل عددی برای RK65 برای h = 0.1 است.
شاخص های برآوردهای ما به طور مطلوب با خطاهای واقعی h = 0.1 (بین 10 -7 -10 -8 ) مقایسه می شود. با این حال، برای h = 0.2، تخمین خطا ما و همچنین راه حل برای h = 0.1، هم بسیار دور از خطاهای واقعی است که خوب است به عنوان دقت است که با افزایش در steplenght کاهش می یابد. بنابراین نتیجه ما با واقعیت سازگار است.
نتیجه گیری
بنابراین می توان نتیجه گرفت که هنگام استفاده از روش های Runge-Kutta برای حل مشکلات غیر سفت، ما نیازی به محاسبه راه حل دقیق نیستیم تا بتوانیم خطاهای را محاسبه کنیم. Extrapolation ریچاردسون یک برآوردگر خطای قابل قبول را فراهم می کند که قادر به ارائه یک ایده کارآمد از ماهیت و درجه اشتباهات است.
همانطور که بیشتر معادلات دیفرانسیلی تحلیلی محلول نیست، راه حل دقیق نمی تواند به دست آید و از این رو امکان اشتباه برای چنین مشکلی ایجاد نمی شود. با این حال، استخراج ریچاردسون یک وسیله عالی برای حل این مشکل است، زیرا برای رسیدن به برآوردهای خطا لازم نیست که راه حل دقیق مورد نیاز باشد.
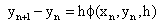

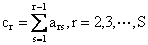




















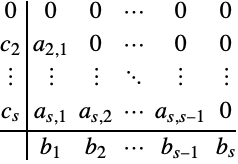








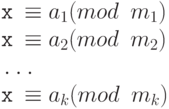
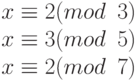
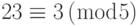
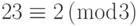
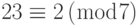

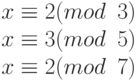
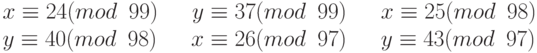







 که همریخت طبیعی هستند
که همریخت طبیعی هستند











 ما پیدا میکنیم :
ما پیدا میکنیم :










 پس
پس  پس
پس  یا
یا
 پس
پس  پس
پس 





 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.