قبل از اینکه این مقاله را مرور کنید ، مطمئن شوید که مقاله قبلی درباره انواع نمودارها را در تئوری نمودار مرور کرده اید .

 

 

ما در این زمینه صحبت کرده ایم-

  • نمودار مجموعه ای از رئوس است که از طریق مجموعه ای از لبه ها به یکدیگر متصل می شوند.
  • مطالعه نمودارها به عنوان تئوری نمودار معروف است .

 

 

در این مقاله ، ما در مورد نمودارهای دو طرفه بحث خواهیم کرد.

 

 

نمودار دو طرفه-

 

نمودار دو بخشی نوع خاصی از نمودار با ویژگی های زیر است -

  • از دو مجموعه راس X و Y تشکیل شده است.
  • رئوس مجموعه X فقط با رئوس مجموعه Y می پیوندند.
  • رئوس موجود در همان مجموعه به هم متصل نمی شوند.

 

نمودار دو طرفه نمودار -

 

نمودار زیر مثالی از نمودار دو بخشی است -

 

 

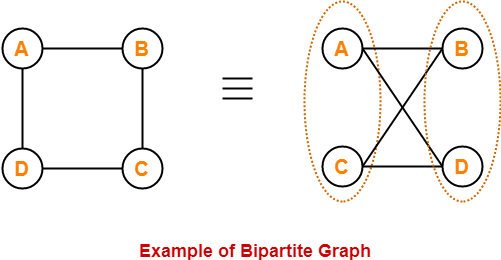
اینجا،

  • رئوس نمودار را می توان به دو مجموعه تجزیه کرد.
  • این دو مجموعه X = {A، C} و Y = {B، D} هستند.
  • رئوس مجموعه X فقط با رئوس مجموعه Y و برعکس می پیوندند.
  • رئوس موجود در همان مجموعه به هم متصل نمی شوند.
  • بنابراین ، این نمودار دو بخشی است.

 

همچنین نمودار - Planar را بخوانید

 

نمودار دو طرفه کامل-

 

یک نمودار کامل دو بخشی ممکن است به شرح زیر تعریف شود -

 

نمودار دو بخشی که در آن هر راس مجموعه X به هر راس مجموعه Y متصل می شود

 

به عنوان نمودار کامل دو بخشی نامیده می شود.

یا

نمودار دو بخشی کامل یک نمودار دو بخشی است که کامل است.

یا

نمودار دو بخشی کامل یک نمودار است که همچنین دو بخشی است و همچنین کامل است.

 

نمودار نمودار دو طرفه را کامل کنید-

 

 

نمودار زیر مثالی از یک نمودار کامل دو بخشی است -

 

 

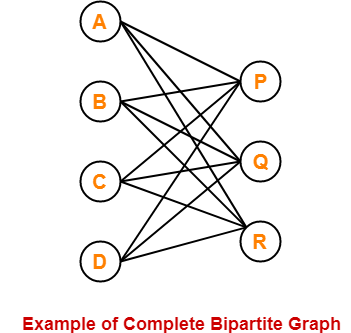
اینجا،

  • این نمودار یک نمودار دو بخشی و همچنین یک نمودار کامل است.
  • بنابراین ، این یک نمودار کامل دو بخشی است.
  • این نمودار K 4،3 نامیده می شود .

 

نمودار رنگی نمودار دو طرفه-

 

برای رنگ آمیزی صحیح هر نمودار دو بخشی ،

  • حداقل 2 رنگ لازم است.
  • این تضمین می کند که رئوس انتهایی هر لبه با رنگ های مختلف رنگ شده اند.
  • بنابراین ، نمودارهای دو بخشی 2 رنگ هستند.

 

توجه داشته باشید

اگر نمودار دو بخشی است و هیچ لبه ای ندارد ، 1 رنگ است.

 

مثال-

 

شماره رنگی نمودار دو بخشی زیر 2 است

 

 

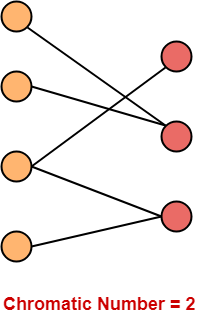
خصوصیات نمودار دو طرفه-

 

چند ویژگی مهم نمودار دو بخشی عبارتند از:

  • نمودارهای  دو بخشی2 رنگی هستند.
  • نمودارهای دو طرفه فاقد چرخه فرد هستند.
  • هر زیر نمودار یک نمودار دو بخشی ، خودش دو بخشی است.
  • هیچ تطبیق کاملی برای نمودار دو بخشی با تقسیم X و Y وجود ندارد اگر | X | | Y |.
  • در هر نمودار دو بخشی با دو بخش X و Y ،

مجموع درجه رأس مجموعه X = مجموع درجه رأس مجموعه Y

 

نمودار تطبیق کامل نمودار دو طرفه-

 

تعداد مسابقات کامل برای K n ، n = n!

 

با توجه به یک نمودار دو بخشی G با دو بخش X و Y ،

  • هیچ تطبیق کاملی برای G وجود ندارد اگر | X | | Y |.
  • یک تطبیق کامل در یک نمودار G دوتایی G با تقسیم X و Y وجود دارد اگر و فقط اگر برای همه زیر مجموعه های X ، تعداد عناصر در زیر مجموعه کمتر یا برابر با تعداد عناصر در همسایگی زیر مجموعه باشد.

 

حداکثر تعداد لبه ها

 

  • هر نمودار دو بخشی متشکل از رئوس 'n' می تواند حداکثر (1/4) xn 2 لبه داشته باشد.
  • حداکثر تعداد ممکن لبه ها در نمودار دو بخشی در رئوس 'n' = (1/4) xn 2 .

 

توضیح

 

  • فرض کنید قسمت تقسیم شده دو نمودار (V 1 ، V 2 ) باشد که در آن | V 1 | = k و | V 2 | = nk
  • تعداد لبه های بین V 1 و V 2 می تواند حداکثر k (nk) باشد که در k = n / 2 به حداکثر می رسد.
  • بنابراین ، حداکثر 1/4 n 2 لبه می تواند وجود داشته باشد.
  • همچنین ، برای هر نمودار G با n راس و بیش از 1/4 n 2 لبه ، G شامل یک مثلث خواهد بود.
  • این در نمودار دو بخشی امکان پذیر نیست ، زیرا نمودارهای دو بخشی حاوی چرخه های عجیب و غریب نیستند.

 

همچنین بخوانید - نمودار اولر و نمودار همیلتونی

 

مسائل عملی براساس گراف دو بخشی در تئوری گراف-

 

مسئله -01:

 

آیا نمودار زیر نمودار دو بخشی است؟

 

 

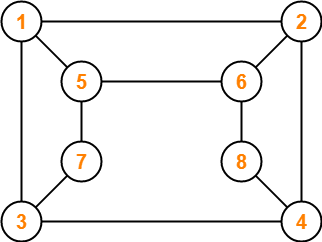
راه حل-

 

نمودار داده شده ممکن است دوباره ترسیم شود -

 

 

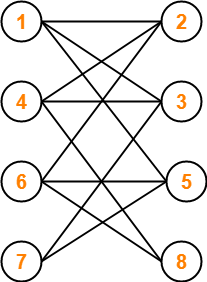
اینجا،

  • این نمودار از دو مجموعه رأس تشکیل شده است.
  • این دو مجموعه عبارتند از X = {1 ، 4 ، 6 ، 7} و Y = {2 ، 3 ، 5 ، 8}.
  • رأس های مجموعه X فقط با رأس مجموعه Y و برعکس پیوند می خورند.
  • همچنین ، هر دو راس درون یک مجموعه به هم متصل نیستند.
  • این تعریف نمودار دو بخشی را برآورده می کند.

 

بنابراین ، نمودار نمودار یک نمودار دو بخشی است.

 

مسئله 02:

 

حداکثر تعداد لبه ها در نمودار دو بخشی در 12 رئوس _________ است؟

 

راه حل-

 

ما می دانیم ، حداکثر تعداد ممکن لبه ها در یک نمودار دو بخشی در رئوس 'n' = (1/4) xn 2 .

 

n = 12 را جایگزین کنید ،

حداکثر تعداد لبه ها در نمودار دو بخشی در 12 رئوس

= (1/4) x (12) ^2

= (1/4) x 12 x 12

= 36

 

 

بنابراین ، حداکثر تعداد لبه ها در یک نمودار دو بخشی در 12 رئوس = 36.

 

 

 

خلاصه

نمودار دو طرفه | مثال نمودار دو طرفه | خواص

نام مقاله

نمودار دو طرفه | مثال نمودار دو طرفه | خواص

شرح

نمودار دو طرفه در تئوری نمودار - نمودار دو طرفه نمودار خاصی است که از 2 مجموعه راس X و Y تشکیل شده است که رئوس فقط از یک مجموعه به مجموعه دیگر می پیوندند. مثال نمودار دو طرفه. خصوصیات نمودار دو طرفه بحث شده است.

نویسنده

آکشی سینگال

نام ناشر

دروازه ویدیالی

آرم ناشر