برای مقالات همگانی، به بررسی توپولوژی (ابهام) .
حلقه موبیوس یک سطح بسته که لبه به حلقهای کاهش می یابد. چنین اشیائی هستند که توسط توپولوژی مورد مطالعه قرار می گیرند.
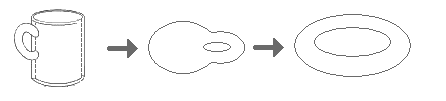
توپولوژی شاخه ای از ریاضیات با مجموعه مجهز به یک مفهوم محله در اطراف هر نقطه، و به نام فضاهای توپولوژیک ، و همچنین برنامه های کاربردی مستمر بین این فضاهای، که حفظ این مفهوم. رسمی، ما در نظر فضاهای تغییر شکل نزدیک بدون پاره شدن و یا چسب، به عنوان یک الاستیک که می توانید بدون شکستن کشش. بنابراین، آن را شناسایی دایره و بیضی ، و یا تاج و دیوار سمت یک سیلندر از انقلاب ، است که می گویند آنها به ترتیبhomeomorphic .
تعریف محله گاهی ناشی از فاصله بین نقاط است که به ساختار فضای متریک منجر می شود . این امر به ویژه از درست خط واقعی از هواپیما ، در فضای سه بعدی ، یا به طور کلی از یک فضای اقلیدسی ، و خود را زیر مجموعه مانند دایره ، در حوزه ، در چنبره و دیگر ریمانی manifolds .
در یک فضای توپولوژیک، مفهوم محله محله را می توان با مفهوم جهانی باز تعریف کرد که محدوده هر یک از نقاط آن است. مجموعه ای از باز نیز "توپولوژی" نامیده می شود. این توپولوژی را می توان با ساختار جبری سازگار کرد ، از این رو تعریف گروه توپولوژی و فضای بردار توپولوژیک ، به ویژه در تجزیه و تحلیل عملکردی .
توپولوژی عمومی مفاهیم و سازه ها برای فضاهای توپولوژیک معمول تعریف می کند. توپولوژی جبری همکاران به هر فضای توپولوژیک از ثابت جبری مانند اعداد ، در گروه های از ماژول یا حلقه که آنها را متمایز، به خصوص در زمینه نظریه گره . توپولوژی دیفرانسیل به مطالعه محدود انواع دیفرانسیل ، که در آن هر نقطه است homeomorphic محله به یک توپ از بعدی متناهی.
خلاصه
اصطلاحات [ ویرایش | کد را تغییر دهید
کلمه "توپولوژی" (یونانی η τοπολογία ) می آید از ترکیبی از دو نام یونانی (ο τοπος ( O TOPOS ، مرد) و η λογία ( من ایوان سرپوشیده ، زنانه) که به ترتیب به معنای "مکان" و "مطالعه" . به معنای واقعی کلمه، توپولوژی به معنی "مطالعه یک مکان" یا "مطالعه موضعی" است. بنابراین، او علاقه مند به تعریف مکان است (همچنین به نام " فضا ") و ویژگی های آن ممکن است. یک علامت باستان، تجزیه و تحلیل موضعی است ، یعنی "مطالعه محل".
اصطلاح "توپولوژی" در سال 1847 توسط آلمانی یوهان برندیچ در Vorstudien zur Topologie به زبان آلمانی منتشر شد .
تاریخچه [ تغییر | کد را تغییر دهید
توپولوژی بر مبنای مفاهیم محدودیت و تداوم استوار است ، ابتدا به توالی واقعی و توابع یک متغیر واقعی اعمال می شود . این مفاهیم از تجزیه و تحلیل از استفاده هجدهم هفتم قرن به خصوص توسطاویلر و لاگرانژ ، اما خواهد شد در رسمی نوزدهم هفتم قرن : کوشی تعریف همگرایی یک دنباله و یا سری ، آبل نشان می دهد که همگرایی یکنواخت و Bolzanoتداوم برای نشان دادن قضیه ارزش متوسط است .
در همان زمان، ریمان معرفی انواع او نام او را، و تبدیل کامل فضاهای مطالعه به عنوان بخشی از توپولوژی دیفرانسیل . درمان های مشترک از این فضاها و آزمون واقعی خواهد در تعریف محله آمدههیلبرت .
در حدود سال 1860، وایرشتراس مفهوم نقطه انباشت را تعریف کرد ، که در تمام مجموعه های نامحدود و محدودی از اعداد حقیقی نشان داد.
هنری پوانکاره در سال 1895 آنالیتسیت را منتشر کرد و مفاهیم هماتومی و همولوگ را معرفی کرد . این invariants به تعداد پذیرش و ویژگی های اویلر (تعریف شده بیش از یک قرن پیش) در آنچه تبدیل خواهد شد توپولوژی جبری .
تنها در 1906 بود، با زور مطالعه مجموعه به طور فزاینده انتزاعی، نظر می رسد مفهوم وجود دارد فضای متریک ، معرفی شده توسط فریشه ، که کار در فضاهای تابع ایالات متحده کانتور ، ولترا ، Arzelà ، Hadamard ، Ascoli و دیگران.
در سال 1914 فلیکس هاستورف مفهوم فضای متریک را به طور کلی به کار برد. او اصطلاح "فضای توپولوژیکی" را تعریف کرد و تعریف کرد که اکنون فضای جداگانه ای یا فضای هادسفورد نامیده می شود .
در نهایت، یکی دیگر از تعاریف جزئی در سال 1922 توسط Kuratowski به مفهوم کنونی فضای توپولوژی اشاره کرد.
توسعه فضاهای بردار نرمال (به ویژه ابعاد بی نهایت) به واسطه هیلبرت است ؛ Banach عمدتا این نظریه را در دهه 1930 تکمیل کرد.
مفهوم یک مجموعه جمع و جور ، جوانه زده در اوایل سال 1900، با کارهای Alexandroff ، Urysohn و Tychonov 1 توسعه یافته است .
بدون بیست و سه مسائل هیلبرت در جنین در اوایل به تن در توپولوژی، هنوز هم xx هفتم قرن . حدس پوانکره است در کانون توجه از هفت مسائل هزاره در سال 2000. این خواهد بود که برای اولین بار به طور کامل توسط نشان پرلمن در آغاز بیست و یکم هفتم قرن با حدس هندسی از ترستون .
بنیانگذار اصول [ ویرایش | کد را تغییر دهید
مفهوم مرکزی در توپولوژی مفهوم محدودیت است . به عنوان مثال یک سطح بسته، یک دیسک را مثال بزنید. از نقطه نظر دقیق تنظیم، نقاطی که در دیسک وجود دارد و کسانی که در آن نیستند وجود دارد. با این حال، این دیدگاه از لحاظ هندسی رضایت بخش نیست. نقاطی که در دایره قرار دارند، محدود کردن دیسک، وضعیت خاصی دارند، آنها در حد محدود هستند . علاوه بر این، در تعریف یک دیسک، ما می توانیم انتخاب کنیم: آیا همه نقاطی را که فاصله آن به مرکز کمتر از یا برابر است، در نظر می گیریم؟به شعاع یا ما همه نقاطی را که فاصله آن به مرکز دقیقا پایینتر از شعاع است، در نظر می گیریم؟ در مورد اول ما می گوییم که دیسک بسته است، در مورد دوم ما می گوییم دیسک باز است. به طور کلی، ما می گوییم که سطح زمانی بسته است که تمام نقطه های آن را شامل می شود . یکی می گوید که سطح باز است اگر برای هر یک از نقاط آن دیسک در این نقطه وجود دارد که در این سطح وجود دارد.
این ایده محدودیت بسیار بصری است. توپولوژی به دنبال این مفهوم است. چند راه برای رسیدن به این هدف وجود دارد. ساده ترین راه تعیین فاصله است . در مثال ما، ما به سادگی از فاصله اقلیدسی استفاده می کنیم. نقاط پایانی آنهایی هستند که در هر دو نقطه در سطح و نقاطی که درون آن نیستند، نزدیک هستند (یعنی، تا آنجا که مایل هستند). تعریف یک فاصله در یک مجموعه به آن یک ساختارفضایی متریک را میدهد. این دیدگاه برای حل بسیاری از مشکلات کافی است با این حال، استفاده از یک پاس از راه دور از طریق اعداد حقیقی و در نتیجه معرفی یک محدودیت که تا به حال برای غلبه بر. برای این کار، آن را تا به لزوم بوده به تعریف مفهوم نزدیکی بیشتر انتزاعی، بدون استفاده از یک آرگومان عددی است مفهوم محله . به دلایل فنی، آن را معادل و ساده به طور مستقیم تعریف قبل از محله های این باز است، بنابراین، این است چگونه معمولا یک توپولوژی در تصمیم گیری چه تعریف می کند قطعات باز .
مفهوم محدود نه تنها استاتیک بلکه پویا نیز است. توپولوژی اجازه می دهد تا محدودیت های توابع و توالی ها را از بین ببریم. بیایید به دنباله ای از inverses از اعداد کامل از 1: 1/1، 1/2، 1/3، 1/4، ...، 1 / n ، ... در حد ، این دنباله به سمت 0. تمایل دارد. این بیشتر به یا کمتر این واقعیت است که 0 نقطه محدود مجموعه ای از 1 / n است .
مهم است که توجه داشته باشیم که اکثر مفاهیم توپولوژی، از جمله تداوم، عواقب مفهوم محدودیت است. این به ویژه در مورد مفهوم مشتق شده است که به عنوان یک حد از نرخ افزایش، از مماس است که محدودیت رشته ها است.
بنابراین توپولوژی یک نظریه متحد است: آن را با چند عاملی اولیه توضیح می دهد تعداد زیادی از پدیده ها.
شاخه های توپولوژی [ ویرایش | کد را تغییر دهید
- توپولوژی عمومی واژگان و یک چارچوب کلی برای برخورد با مفاهیم فراهم می کند حد ، از تداوم و محله .
- ایده توپولوژی جبری متشکل از همبستگی متغیرهای مختلف با فضاهای مختلف به منظور طبقه بندی آنها است. اولین موجودات کشف شده دیجیتال بودند. امروزه این invariants ساختارهای جبری، گروه ها ، حلقه ها ، اغلب اوقات است. مکاتبات بین فضاها و اشیا ها فاکتورها هستند و تئوری دسته ها گاهی درک این را ساده می کند. در میان دیگران، گروه اساسی و هماهنگی منحصر بهفرد وجود دارد .
- توپولوژی دیفرانسیل مورد مطالعه خواص توپولوژیکی از منیفولدهای دیفرانسیل و خود درونه گیریها و immersions در فضای اقلیدسی.
- توپولوژی هندسی مطالعه انواع و برنامه های کاربردی با هم، به خصوص انواع نرخهای پایین در دیگری است. یک شاخه فعال خاص، توپولوژی کم ابعادی است که در مورد انواع ابعاد کمتر از 4 یا برابر است و شامل نظریه گره ها است .
- از آنجا که 50 سال و با نفوذ سمینار هندسه جبری ماری چوب از الکساندر Grothendieck ، توپولوژی در حال حاضر به طور گسترده تر به عنوان مطالعه تعریف TOPOS .






 ، زیر مجموعه ای از X × Y است .
، زیر مجموعه ای از X × Y است .
 در X بسته است این شرح است که اگر Y هاسدورف است و F و G در دیدن همه موارد
در X بسته است این شرح است که اگر Y هاسدورف است و F و G در دیدن همه موارد 


 ، دقیقا به طور دقیق به طور منظم نامیده می شود در صورتی که نقاط می توانند از مجموعه های بسته از طریق (محدود) توابع واقعی پیوسته پیوسته
، دقیقا به طور دقیق به طور منظم نامیده می شود در صورتی که نقاط می توانند از مجموعه های بسته از طریق (محدود) توابع واقعی پیوسته پیوسته  و هر
و هر  ، پس از آن
، پس از آن  به طوری که
به طوری که  و
و  . (به طور برابر می توان هر دو مقدار را به جای آن انتخاب کرد
. (به طور برابر می توان هر دو مقدار را به جای آن انتخاب کرد و
و  و حتی خواستار آن هستیم
و حتی خواستار آن هستیم  یک تابع محدود باشد.)
یک تابع محدود باشد.)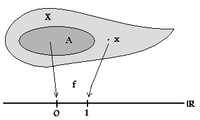


 تابع عضویت
تابع عضویت  می تواند به عنوان یک خانواده در نظر گرفته شود
می تواند به عنوان یک خانواده در نظر گرفته شود ![{\ displaystyle \ mu _ {A} = (\ mu_ {A} (x)) _ {x \ in {U}} \ in [0،1] ^ {U}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39a1769d64a2d88ed6d1e98f0d91bbb6e343c5e0) . دومی یک
. دومی یک  شناخته شده. متریک را می توان از یک
شناخته شده. متریک را می توان از یک  از طریق
از طریق .
. محدود است، یعنی
محدود است، یعنی  ، چنین متریک ممکن است توسط:
، چنین متریک ممکن است توسط: جایی که
جایی که  و
و  توالی واقعی numbes بین 0 و 1 هستند.
توالی واقعی numbes بین 0 و 1 هستند. ،
،
 و
و ) ممکن است از فاصله فاصله بگیرد، به عنوان مثال پس از پیشنهاد Koczy:
) ممکن است از فاصله فاصله بگیرد، به عنوان مثال پس از پیشنهاد Koczy: اگر
اگر محدود است
محدود است اگر
اگر  یک پارامتر شیب دار و
یک پارامتر شیب دار و  .
.  توسط Beg و اشرف نیز ارائه شده است.
توسط Beg و اشرف نیز ارائه شده است.  از یک نوع خاص؛ معمولا این مورد مورد نیاز است
از یک نوع خاص؛ معمولا این مورد مورد نیاز است - درجه عضويت x
- درجه عضويت x - درجه عدم عضویت در x
- درجه عدم عضویت در x![{\ displaystyle \ mu _ {A}، \ nu _ {A}: U \ mapsto [0،1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/719e67f28fe95d4c1755813f7afe1995b1716baf)

 رای دادن
رای دادن )،
)، )،
)، )
)![{\ displaystyle D ^ {*} = \ {(\ alpha، \ beta) \ in [0،1] ^ {2} \ mid \ alpha + \ beta = 1 \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db86788e2546eed1bcf7769457721e872fad0b09) و با ترکیب هر دو توابع به
و با ترکیب هر دو توابع به این وضعیت شبیه نوع خاصی از مجموعه های فازی L است.
این وضعیت شبیه نوع خاصی از مجموعه های فازی L است. ، "درجه عضویت مثبت"، "درجه عضویت بی طرف"، و "درجه عضویت منفی" و شرایط اضافی
، "درجه عضویت مثبت"، "درجه عضویت بی طرف"، و "درجه عضویت منفی" و شرایط اضافی این به وسیلۀ امكان اضافی «امتناع از رای گیری»، نمونه رأی گیری را بالا می برد.
این به وسیلۀ امكان اضافی «امتناع از رای گیری»، نمونه رأی گیری را بالا می برد.![{\ displaystyle D ^ {*} = \ {(\ آلفا، \ بتا، \ گاما) \ در [0،1] ^ {3} \ اواسط \ آلفا + \ بتا + \ گاما = 1 \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/823d51898a57e22f63d2a9b38b3b6b43822197b6) و خصوصیات "فازی عکاسی"، t- و s-norms این مشابه نوع دیگری از مجموعه های فازی L است.
و خصوصیات "فازی عکاسی"، t- و s-norms این مشابه نوع دیگری از مجموعه های فازی L است.  :
: اگر
اگر 
 دارای حداکثر منحصر به فرد است
دارای حداکثر منحصر به فرد است
 اگر
اگر برای
برای  و
و برای
برای  ،
،
 ،
،

 است
است ![{\ displaystyle S (\ alpha) = - \ alpha \ ln \ alpha - (1- \ alpha) \ ln (1- \ alpha)، \ alpha \ in [0،1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bd4132e4bd7ebcf25a1ddf6149c097503d57c9d)
 ثابت است بسته به واحد اندازه گیری و پایه لگاریتم (
ثابت است بسته به واحد اندازه گیری و پایه لگاریتم ( 






 جایی که
جایی که ![{\ displaystyle m \ colon U \ rightarrow [0،1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d2ca07bd2c46e39ef87ed3ce24798d5235c3cf3) یک تابع عضویت مجموعه مرجع
یک تابع عضویت مجموعه مرجع یا
یا  ارزش
ارزش  درجه عضویت عضویت نامیده می شود
درجه عضویت عضویت نامیده می شود تابع عضویت از مجموعه فازی نامیده می شود
تابع عضویت از مجموعه فازی نامیده می شود .
. مجموعه فازی
مجموعه فازی
 سپس
سپس (بدون عضو)
(بدون عضو) (عضو کامل)
(عضو کامل) (عضو فازی).
(عضو فازی). 
![\ alpha \ in [0،1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/daf3c62599ea71319c85f715c9e590d2bab2d036) مجموعه های شفاف زیر تعریف می شوند:
مجموعه های شفاف زیر تعریف می شوند: است که به نام خود -α قطع
است که به نام خود -α قطع  آن را α-cut قوی (به عنوان مثال سطح قوی سطح α نامیده می شود)
آن را α-cut قوی (به عنوان مثال سطح قوی سطح α نامیده می شود) پشتیبانی آن نامیده می شود
پشتیبانی آن نامیده می شود هسته آن (یا گاهی هسته ) نامیده می شود
هسته آن (یا گاهی هسته ) نامیده می شود  )
)![[0، 1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
 ،
، مقادیری را در بعضی از
مقادیری را در بعضی از  . بسیاری از
. بسیاری از (یعنی، آن شامل تنها دو عنصر است)، مجموعه فازی را می توان به عنوان یک مجموعه منظم در نظر گرفت.
(یعنی، آن شامل تنها دو عنصر است)، مجموعه فازی را می توان به عنوان یک مجموعه منظم در نظر گرفت. و
و ![M = [0،1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c27b72eed1a041bb45eb36f141bc163e4f962183) . سپس:
. سپس: ؛
؛ ارتفاع یک مجموعه فازی نامیده می شود
ارتفاع یک مجموعه فازی نامیده می شود . مجموعه فازی
. مجموعه فازی . اگر ارتفاع به شدت کمتر باشد
. اگر ارتفاع به شدت کمتر باشد . یک مجموعه فازی غیرمعمول غیر نامطلوب می تواند با استفاده از فرمول normalized شود
. یک مجموعه فازی غیرمعمول غیر نامطلوب می تواند با استفاده از فرمول normalized شود ؛
؛ فقط بر روی یک
فقط بر روی یک  از
از  برای که
برای که  نقاط انتقال یک مجموعه فازی نامیده می شود
نقاط انتقال یک مجموعه فازی نامیده می شود مجموعه های فازی در یک مجموعه جهانی تعریف شده است
مجموعه های فازی در یک مجموعه جهانی تعریف شده است  .
. نه برای همه
نه برای همه 
 .
. .
. تقریبا برابر با یکدیگر است، صحبت در مورد درجه برابری مجموعه های فازی
تقریبا برابر با یکدیگر است، صحبت در مورد درجه برابری مجموعه های فازی
 .
. ، مجموعه ای از موارد زیر نامیده می شود :
، مجموعه ای از موارد زیر نامیده می شود : ،
،
 .
. است محدب اگر و تنها اگر شرایط زیر:
است محدب اگر و تنها اگر شرایط زیر:![{\ displaystyle \ mu_ {A} [\ gamma x_ {1} + (1- \ gamma) x_ {2}] \ geqslant \ langle \ mu_ {A} (x_ {1}) \ land \ mu_ { A} (x_ {2}) = \ min \ {\ mu_ {A} (x_ {1})، \ mu_ {A} (x_ {2}) \} \ rangle}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f4758765a73c074ebcd0bbae05d29efcf082909)
 و
و ![{\ displaystyle \ gamma \ in [0،1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbc65bc4fa0e25a8305259b234865def64ac1a8a) .
.![{\ displaystyle \ mu_ {A} [\ gamma x_ {1} + (1- \ gamma) x_ {2}] \ leqslant \ langle \ mu_ {A} (x_ {1}) \ lor \ mu_ { A} (x_ {2}) = \ max \ {\ mu_ {A} (x_ {1})، \ mu_ {A} (x_ {2}) \} \ rangle}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36284f7a161c9de41235f42da97a521273c24cf4)
![M = [0،1] \](https://wikimedia.org/api/rest_v1/media/math/render/svg/370e4fd9016f3e8ff789a7a94923b844f5d11d92)
 .
. .
. .
. .
. با عملکرد جانبی:
با عملکرد جانبی: برای هر
برای هر  ،
، - این به اصطلاح
- این به اصطلاح 



![{\ displaystyle \ mu _ {A \ cap B} (x) = 1 \ min \ {1، [(1 \ mu_ {A} (x)) ^ {p} + (1- \ mu_ { B} (x)) ^ {p}] ^ {1 \ over p} \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf4ee0c2e7259470fc28a19338162afc4f2a2dcd) برای
برای
 ،
،



![{\ displaystyle \ mu _ {A \ cup B} (x) = \ min \ {1، [\ mu_ {A} ^ {p} (x) + \ mu_ {B} ^ {p} (x) ] ^ {1 \ over p} \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e59eb2e4e3fcf7beae9c4dd82b86b774a3c722c9) برای
برای  .
.




 . خروجی DSFT است
. خروجی DSFT است  جایی که T فاصله بین نمونه ها است.
جایی که T فاصله بین نمونه ها است.![{\ displaystyle L [y] = y ^ {(n)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55748cdb64e2e70170550b1601827405a7391b16)
![{\ displaystyle L [y] = \ int _ {a} ^ {t} y \، dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb616ec3149c278d4ed4d471906c2f3e485248a6)


![{\ displaystyle L [y] = y \ circ f}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adf8e1a8de11d2b9a58113939186edfd36eb5b78)
![{\ displaystyle L [y] = {\ frac {y \ circ t + y \ circ -t} {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4053efbb3a2417b0187252ce8ce11943d1811df1)
![{\ displaystyle L [y] = {\ frac {y \ circ ty \ circ -t} {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aea9dbfed39f54e300c1b0ecb00212a12c0bb5d8)
![{\ displaystyle L [y] = y \ circ (t + 1) -y \ circ t = \ Delta y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a59c37d0103cd9e45f3008be15be307a2121318b)
![{\ displaystyle L [y] = y \ circ (t) -y \ circ (t-1) = \ nabla y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/285cc671ff18fcea194db0b07bef7943c5cc718f)
![{\ displaystyle L [y] = \ sum y = \ Delta ^ {- 1} y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2734b315faf5301c1b49a3d1920dd6b1bb4b378)
![{\ displaystyle L [y] = - (py ')' + qy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec732fb50af69f011ca9eca0fc1fc8156cfc954c)
![{\ displaystyle F [y] = y ^ {[- 1]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e505c0ad5eebe33b1d91e82cada72c95c09d04c9)
![{\ displaystyle F [y] = t \، y '^ {[- 1]} - y \ circ y' ^ {[- 1]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e3ef79233c2a76b9e7a6b2fe1ab9bd690af7e5a)
![{\ displaystyle F [y] = f \ circ y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e5c7044beca35c385f28f9684ef56ccedcb4fc2)
![{\ displaystyle F [y] = \ prod y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6db0139615cdc804309a1e7360c50e6aeae0256e)
![{\ displaystyle F [y] = {\ frac {y}} {y}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be39d46a4b51569e8fd4e481ed2935f4ae3e2197)
![{\ displaystyle F [y] = {\ frac {ty '} {y}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33bad35cb3771f86c734f0123676152bae90fde6)
![{\ displaystyle F [y] = {y '' \ over y '} - {3 \ over 2} \ left {{y \' y over} \ right} ^ {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82429a931a7be02e43c48a978c443a08f7563a1f)
![{\ displaystyle F [y] = \ int _ {a} ^ {t} | y '| \، dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2759c4bc022e78e98f4215212344e0abfa4f474d)
![{\ displaystyle F [y] = {\ frac {1} {ta}} \ int _ {a} ^ {t} y \، dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5dbf8b880776c6738161e718a19a80cb010d6f8)
![{\ displaystyle F [y] = \ exp \ left ({\ frac {1} {ta}} \ int _ {a} ^ {t} \ ln y \، dt \ right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f002952416bda45b3935e147ad3dbe8a88423e6)
![{\ displaystyle F [y] = - {\ frac {y} {y '}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b744a33e05acd24dc342902fc4435f9b98cc02b)
![{\ displaystyle F [x، y] = - {\ frac {yx '} {y'}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf503f7c4cfe9a01ed4600ce99056a44c0ddcbb5)


![{\ displaystyle F [r] = - {\ frac {r ^ {2}} {r '}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b8c3e99b9a9d37d6709af9ebc75662c4894e1f9)


![{\ displaystyle F [r] = {\ frac {1} {2}} \ int _ {a} ^ {t} r ^ {2} dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05bffb44214252eaa080593550c1fadb19f401a1)
![{\ displaystyle F [y] = \ int _ {a} ^ {t} {\ sqrt {1 + y} ^ {2}}} \، dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7f5075734f6fe703a7580c22819a9bdc4fd8628)
![{\ displaystyle F [x، y] = \ int _ {a} ^ {t} {\ sqrt {x '^ {2} + y' ^ {2}}} \، dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a6ca40e6175c2bb3c7322c838a57f33a2f2ec39)
![{\ displaystyle F [r] = \ int _ {a} ^ {t} {\ sqrt {r ^ {2} + r '^ {2}}} \، dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c184b7ab8977f6a6edc027a9e1acdada1974ea0)
![{\ displaystyle F [x، y] = \ int _ {a} ^ {t} {\ sqrt [{3}] {y '}} \، dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/504521ea56723619d39b051ff35e4e9fd6b40ca5)
![{\ displaystyle F [x، y] = \ int _ {a} ^ {t} {\ sqrt [{3}] {x'y '' - x''y '}} \، dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47508e30fcd4d476900960eb4f84b3c1295c0ae7)
![{\ displaystyle F [x، y، z] = \ int _ {a} ^ {t} {\ sqrt [{3}] {z '' '(x'y' '- y'x' ') + z '' (x '' 'y'-x'y' '') + z '(x''y' '' - x '' '' y '')}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b20a01bc6a9e37354edadf6b24e14f6c51dbb5f9)

![{\ displaystyle F [y] = {\ frac {y}} {(1 + y '^ {2}) ^ {3/2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2733d361692921c78d8491e12ff0d3975e46672e)
![{\ displaystyle F [x، y] = {\ frac {x'y '' - y'x ''} {{x '^ {2} + y' ^ {2}) ^ {3/2}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/0092d291416fcd260b739fa7015c28619ee93702)
![{\ displaystyle F [r] = {\ frac {r ^ {2} + 2r '^ {2} -rr' '} {{r ^ {2} + r' ^ {2}) ^ {3/2} }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfa7d7dbbee040a4d5826ba4ab9f7cb82ce65a18)
![{\ displaystyle F [x، y، z] = {\ frac {\ sqrt {(z''y'-z'y '') ^ {2} + (x''z'-z''x ') ^ {2} + (y''x'-x''y ') ^ {2}}} {(x' ^ {2} + y '^ {2} + z' ^ {2}) ^ {3 / 2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5207fd18045bcdfa79d3df3e0f09fea7d962d443)
![{\ displaystyle F [y] = {\ frac {1} {3}} {\ frac {y '' '} {(y' ') ^ {5/3}}} - {\ frac {5} { 9}} {\ frac {y '' '^ {2}} {(y' ') ^ {8/3}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e7a3650eaa04be655adc42c3346eb29358961ee)
![{\ displaystyle F [x، y] = {\ frac {x''y '' '- x' '' y ''} {{x'y '' - x''y ') ^ {5/3} }} - {\ frac {1} {2}} \ left [{\ frac {1} {(x'y '' - x''y ') ^ {2/3}}} \ right]' '}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a69d739b8216cae91fad1ca47b9e723093682d8)
![{\ displaystyle F [x، y، z] = {\ frac {z '' '(x'y' '- y'x' ') + z' '(x' '' y'-x'y '' ') + z' (x''y '' '- x' '' y '')} {(x '^ {2} + y' ^ {2} + z '^ {2} ^ {2} + y '' ^ {2} + z '' ^ {2})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2173260d52b59f35d1d713a8378669f8e5a494b)
![{\ displaystyle X [x، y] = {\ frac {y '} {yx'-xy}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b267261ce0de1ba0a6ca53134308e5a263da24d1)
![{\ displaystyle Y [x، y] = {\ frac {x}} {xy'-yx}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/547f7562b2770e9c54b89f99e4b9ad2b1d9ede0f)
![X [x، y] = x + \ frac {ay}} {\ sqrt {x '^ 2 + y' ^ 2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7049a1a66ae0e3a174a1953af510094495b5a2e)
![{\ displaystyle Y [x، y] = y - {\ frac {ax}} {\ sqrt {x '^ {2} + y' ^ {2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7b555b5ef64340d7b8110451e067703a405d379)
![{\ displaystyle X [x، y] = x + y '{\ frac {x' ^ {2} + y '^ {2}} {x''y'-y''x'}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/863007693180945db748fccf523a900cd172d85d)
![{\ displaystyle Y [x، y] = y + x '{\ frac {x' ^ {2} + y '^ {2}} {y''x'-x''y}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b73ec650428cdcc8f03cb9444aee9b49b6dcf05)
![{\ displaystyle F [r] = t (r '\ circ r ^ {[- 1]})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3562fadfb34e7d19384e119e1f01f1d57ee84b2)


![{\ displaystyle X [x، y] = x - {\ frac {x} \ int _ {a} ^ {t} {\ sqrt {x '^ {2} + y' ^ {2}}} \، dt } {\ sqrt {x '^ {2} + y' ^ {2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/203e22b2482eac10aaea0446f9a3e69e82db9674)
![{\ displaystyle Y [x، y] = y - {\ frac {y '\ int _ {a} ^ {t} {\ sqrt {x' ^ {2} + y '^ {2}}} \، dt } {\ sqrt {x '^ {2} + y' ^ {2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9f2233dc9b36793a05d1afd06e88265b393567b)
![X [x، y] = {\ frac {(xy'-yx ') y'} {x '^ {2} + y' ^ {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db71b35d67e2606dcf3a05acce73dc9193767cb6)
![{\ displaystyle Y [x، y] = {\ frac {(yx'-xy ') x'} {x '^ {2} + y' ^ {2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39388d40e20824a70c17f7a32237033623ba7439)
![{\ displaystyle X [x، y] = {\ frac {(x '^ {2} -y' ^ {2}) y '+ 2xyx'} {xy'-yx}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5c924853b4907ed4da8a2ac246d9580e8bc44f8)
![{\ displaystyle Y [x، y] = {\ frac {(x '^ {2} -y' ^ {2}) x '+ 2xyy'} {xy'-yx}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79fe316c48155e6f92993f1e3c1393c47e30699c)
![{\ displaystyle X [y] = \ int _ {a} ^ {t} \ cos \ left [\ int _ {a} ^ {t} {\ frac {1} {y}} \، dt \ right] dt }](https://wikimedia.org/api/rest_v1/media/math/render/svg/935c78f92c71c500905f0e5eb20097dbffb1f5d0)
![{\ displaystyle Y [y] = \ int _ {a} ^ {t} \ sin \ left [\ int _ {a} ^ {t} {\ frac {1} {y}} \، dt \ right] dt }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ed7d68b49a43d3e04780d4f006de948ae7216e1)

![{\ displaystyle F [y] = \ | y \ | = {\ sqrt {\ int _ {E} y ^ {2} \، dt}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4017443e893dd3adb4e88cc75417d5b01ccc16e0)
![{\ displaystyle F [x، y] = \ int _ {E} xy \، dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/802878f8dc672ed389e2eb52e0260cbedbf0f738)
![{\ displaystyle F [x، y] = \ arccos \ left [{\ frac {\ int _ {E} xy \، dt} {{sqrt {\ int _ {E} x ^ {2} \، dt} } {\ sqrt {\ int _ {E} y ^ {2} \، dt}}}} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab83c107b4f06a04bf00c6b25aea41968897760d)
![{\ displaystyle F [x، y] = x * y = \ int _ {E} x (s) y (ts) \، ds}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7eacc479d5118751b7e740e1e4383ee523604d3a)
![{\ displaystyle F [y] = \ int _ {E} y \ ln y \، dy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7de917a419d0581d0ec95802d0b01a13571d2051)
![{\ displaystyle F [y] = \ int _ {E} yt \، dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c320e540a14d41266a5d973b60b214075ef63b40)
![{\ displaystyle F [y] = \ int _ {E} \ left (t- \ int _ {E} yt \، dt \ right) ^ {2} y \، dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1324142b0ca262523919913e4949fe2a0a7be9c5)


 ، جایی که
، جایی که .
.
 با یک مجموعه باز و F کلاس{\ displaystyle {\ mathcal {C}} ^ {2}}
با یک مجموعه باز و F کلاس{\ displaystyle {\ mathcal {C}} ^ {2}} سپس ماتریس هسیان به خوبی تعریف شده است و طبق قضیه
سپس ماتریس هسیان به خوبی تعریف شده است و طبق قضیه  یک مجموعه باز و {\ displaystyle f \ colon A \ to \ mathbb {R}}
یک مجموعه باز و {\ displaystyle f \ colon A \ to \ mathbb {R}} یک تابع با مشتقات پیوسته دوم:
یک تابع با مشتقات پیوسته دوم: این است که به
این است که به  ماتریس Hessian {\ displaystyle H_ {f} (a) \،}
ماتریس Hessian {\ displaystyle H_ {f} (a) \،} این
این  اگر یک برنامه خطی مداوم وجود دارد، تمایزپذیر است {Y)}
اگر یک برنامه خطی مداوم وجود دارد، تمایزپذیر است {Y)} چنین است:
چنین است:

 این فضاپیما فضایی دیگر را با هنجار تنظیم می کند:
این فضاپیما فضایی دیگر را با هنجار تنظیم می کند:




 ، جایی که
، جایی که  مجموعه ای از متغیرها است
مجموعه ای از متغیرها است مجموعه ای از مقادیر مربوطه است و
مجموعه ای از مقادیر مربوطه است و مجموعه ای از محدودیت ها است.
مجموعه ای از محدودیت ها است. می تواند مقادیری را در دامنه غیر قابل نفوذ بگیرد
می تواند مقادیری را در دامنه غیر قابل نفوذ بگیرد  . هر محدودیتی
. هر محدودیتی به نوبه خود یک جفت است
به نوبه خود یک جفت است  ، جایی که
، جایی که یک زیر مجموعه از
یک زیر مجموعه از هست یک در
هست یک در  . ارزیابی از متغیرهای یک تابع از یک زیر مجموعه از متغیرها به یک مجموعه خاص از ارزش ها در زیر مجموعه مربوطه از حوزه است. ارزیابی
. ارزیابی از متغیرهای یک تابع از یک زیر مجموعه از متغیرها به یک مجموعه خاص از ارزش ها در زیر مجموعه مربوطه از حوزه است. ارزیابی یک محدودیت را برآورده می کند
یک محدودیت را برآورده می کند  رابطه را ارضا می کند
رابطه را ارضا می کند 


 نشان دهنده بردار (x 1 ، x 2 ) است.
نشان دهنده بردار (x 1 ، x 2 ) است. کمترین مقدار دارد. اما این راه حل محدودیت ها را برآورده نمی کند. راه حل مشکل
کمترین مقدار دارد. اما این راه حل محدودیت ها را برآورده نمی کند. راه حل مشکل  که نقطه ای با کوچکترین ارزش است
که نقطه ای با کوچکترین ارزش است 








 راه حل نامزدی با استفاده
راه حل نامزدی با استفاده  این راه حل نامزدی در حقیقت درست است مگر زمانی که
این راه حل نامزدی در حقیقت درست است مگر زمانی که 
 است
است 
 انتظار می رود بیش از همه ارزش های جمعیتی X ، dP θ یک
انتظار می رود بیش از همه ارزش های جمعیتی X ، dP θ یک 
 برآورد θ و تابع افت محدوده است
برآورد θ و تابع افت محدوده است




![{\ displaystyle {\ underset {\ delta} {\ operatorname {arg \، min}}} \ operatorname {E} _ {\ theta \ in \ Theta} [R (\ theta، \ delta)] = {\ underset { \ delta} {\ operatorname {arg \، min}}} \ \ int _ {\ theta \ in \ Theta} R (\ theta، \ delta) \، p (\ theta) \، d \ theta.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/118ed61f14f1d53953242831140397d033eb052d)
 ، و
، و  . با این وجود فقدان مطلق دارای نقایصی است که در تمایز آن وجود ندارد
. با این وجود فقدان مطلق دارای نقایصی است که در تمایز آن وجود ندارد . از دست دادن مربع است که نقطه ضعف آن است که تمایل به تحت سلطه می شود
. از دست دادن مربع است که نقطه ضعف آن است که تمایل به تحت سلطه می شود 
 )، مبلغ نهایی به دلیل یک عدد بزرگ به ویژه یک بزرگنمایی، به جای بیان یک میانگین، یک ارزش است .
)، مبلغ نهایی به دلیل یک عدد بزرگ به ویژه یک بزرگنمایی، به جای بیان یک میانگین، یک ارزش است .

 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.